Modèle hyperbolique de Poincaré
III. Cercle et distance

III.5.c - Tangentes communes à deux cercles

[III.5.a. Tangente à un cercle] [III.5.b. Lieu des centres des tangentes à un cercle] 

[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 Médiatrice, milieu ...] [III.4 - Horocycles] [III.6 - Premières utilisations]

[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]

[Retour aux GNE] [Menu général]

 

Le lieu des centres des tangentes à un cercle étant une conique que nous avons construite de manière stable à la page précédente, le centre des tangentes communes à deux cercles est à l'intersection de ces coniques. Le reste est affaire de gestion d'implémentation de Cabri ...

 

Figure et macros finales

  HCrcl24.fig ou THComExt.mac ou THComInt.mac

Dans la figure ci-dessus les cercles sont euclidiens. Les deux points verts sont leurs centres hyperboliques. Les tangentes communes de même type (en bleu, contacts "Int-Int" ou "Ext-Ext") sont données par la macro THComExt.mac, celles de type différents (contacts "Int-Ext" en marron) par la macro THComInt.mac. Dans la troisième illustration, on voit que les tangentes de "même type" peuvent être des arcs de cercle tangents extérieurement ou intérieurement. C'est la raison pour laquelle, s'il y a deux tangentes d'un même type, pour la construction Cabri, il y a deux couples d'arcs de cercle, ce qui n'est pas tout à fait satisfaisant, si on voulait pousser plus loin des constructions avec ces tangentes communes. Pour être clair, les deux arcs bleus les plus proches du centre de l'horizon dans les illustrations 1 et 3 ne sont pas les mêmes objets Cabri, ils existent même exclusivement l'un de l'autre.

Le reste de la page détaille la construction sur la base de l'intersection de deux coniques. On commence par une approche perceptive, puis on aborde la construction proprement dite.

 

Approche perceptive

 

a - il y a (en général) 4 tangentes communes à deux cercles

 

 

HCrcl25.fig
 

b - Centre des tangentes comme intersection de 3 coniques

En effet, les centres des tangentes communes sont les intersections des deux coniques des centres des tangentes à chaque cercle (ci-dessous bleue et orange). On peut affiner en cherchant lesquelles de ces intersections vont produire les tangentes "extérieures" et "intérieures". Pour cela, il suffit d'écrire qu'un point M est centre d'un cercle tangent aux deux cercles de centre A et B, de rayon rA et rB, de manière extérieure ou non. Avec Cabri, cela donne l'illustration suivante, où l'on voit bien que les intersections des coniques des centres des tangentes passent aussi par deux autres coniques (ci-dessous marron et rose), ce qui permet de distinguer les deux types de tangentes : 

 

HCrcl26.fig

 

Toutefois, on sait que les intersections des coniques dans Cabri II ne sont pas dynamiquement bien séparées, du moins au moment de la rédaction de ces pages (06/98). Il va donc falloir être un peu attentif pour réaliser des constructions dynamiques fiables.

Pour cela on utilisera une remarque de Pierre Delezoïde - qu'il soit ici remercié pour cette information salvatrice - en observant que deux coniques bifocales ayant un foyer commun ont leurs intersections constructibles à la règle et au compas (voir la page d'exos correspondante ou la solution) : ouf, on va pouvoir réaliser des constructions simples et efficaces.

 

Construction effective

a - les problèmes rencontrés

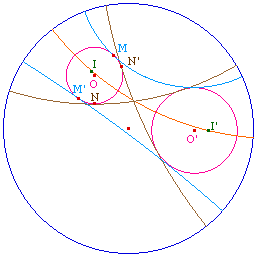
Prenons le cas d'un centre de tangentes communes de même type - plus rapidement "extérieures", M ci-contre. Dans le cas rB > rA, M vérifie MB - MA = rB - rA. Donc M est sur la conique de foyer A, de cercle directeur le cercle de centre B de rayon rB - rA, et sur cette conique, il est sur la branche du côté de A : d'où le point I sur la méditrice de [AB] qui conditionne le cercle support de la tangente commune.

Sur cette même hyperbole, un point N serait centre d'une tangente commune de même type mais avec deux contacts intérieurs, il vérifierait NA - NB = rB - rA, donc il serait sur l'autre branche de la conique (non visible ci-contre).

Si on ne prend pas garde aux branches, et que l'on travaille directement sur la conique |MA - MB&endash; = |rB - rA| on aboutit automatiquement à des figures Cabri qui ne rendent pas compte de tous les cas dynamiques car, quand une tangente commune franchi le centre de l'horizon, d'un contact "Ext-ext" par exemple, elle passe aux contacts "Int-int" et réciproquement, ce qui correspond, dans Cabri, obligatoirement à un changement d'arc.

Remarque : cela ne signifie pas que l'on ne pourrait pas rendre un seul arc pour tous les cas - en macro - mais alors il faudrait particulièrement travailler des questions logiques non triviales, ce qui ne sera pas fait ici, pour celle première livraison ...

Il résulte de cette première analyse qu'il est préférable de travailler avec des copies des cercles dont on sait lequel est le plus petit et lequel est le plus grand pour éviter les valeurs absolues et distinguer alors correctement les branches d'hyperbole. Ceci est possible avec la macro Compar2C.mac détaillée à la page Compar3C.html de la rubrique Alice.

Pour information, cette technique a déjà été utilisée dans abraCAdaBRI aux pages TExt2CAm.html, pour des tangentes communes dynamiques à deux cercles euclidiens, et VieteDynamik.html, pour une solution dynamique de la construction de Viète des 8 cercles tangents à 3 cercles donnés.

b - figure initiale

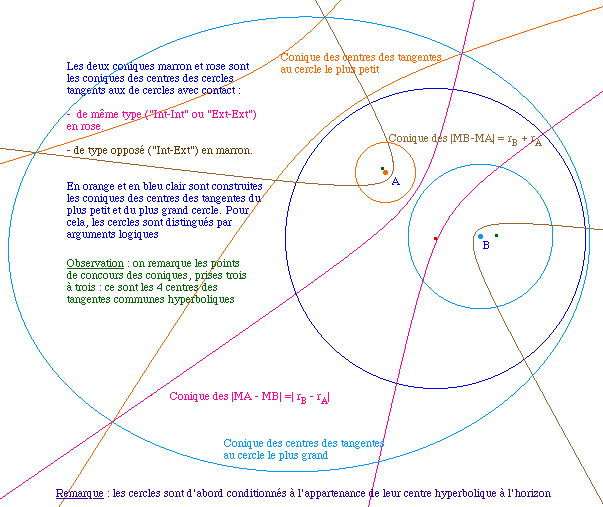
Sous les deux cercles de centre A et B, on commence par construire, à partir de l'existence de leur centre hyperbolique IA et IB, des cercles qui n'existent que si les cercles sont à l'intérieur du disque de Poincaré. Sur ces deux nouveaux cercles est alors appliquée la macro Compar2C.mac qui donne le cercle orange - le plus petit - de centre CInf et le cercle bleu - le plus grand - de centre CSup. Tous les traitements se feront ensuite sur ces deux derniers cercles.

Puis la macro CdirCnkT.mac qui renvoie le cercle directeur C de la conique des centres des tangentes hyperbolique à un cercle est appliquée au petit cercle, de centre CInf.

Enfin, on construit les deux cercles de centre CSup, de rayon la différence des deux rayons (C') et la domme des rayons (C"), cercles en vert ci-contre.

HCrcl27a.fig

c - Traitement du cas "Ext-ext"

Sur le cercle directeur de la conique des centres des tangentes au petit cercle - le cercle C - on construit, par la macro Deux contacts de même type ( ContMT.mac - de la page BFSolP02.html ) appliquée à CInf, C et C', les points du cercle C qui générent les points communs à la conique de foyer CInf de cercle directeur C et celle de foyer CInf de cercle directeur C'. Cette macro donne deux points T et T'. La droite passant par T et le centre de C coupe la médiatrice de [T CInf] en M. Ce point M est centre d'une tangente commune extérieure (type "Ext-Ext") ssi il est du même côté que Cinf de l'hyperbole, c'est-à-dire de l'autre côté que CSuf par rapport à la médiatrice de [Cinf CSup] (aussi axe non focale de l'hyperbole).

 

HCrcl27b.fig

Soit alors I l'intersection de cette médiatrice avec le segment [Csup M]. On conditionne, par la macro Ping-Pong (PingPong.mac) l'intersection du segment [CInf M] avec l'intersection du petit cercle (orange) à celle de I, ce qui donne le point K. Le cercle de centre M passant par K est alors toujours - quand il existe - la trace d'une tangente hyperbolique commune aux deux cercles. On fait de même avec le point T'. (On pourrait faire un symétrique hyperbolique par rapport à la droite hyperbolique des centres hyperboliques (II').

d - Traitement du cas "Int-int"

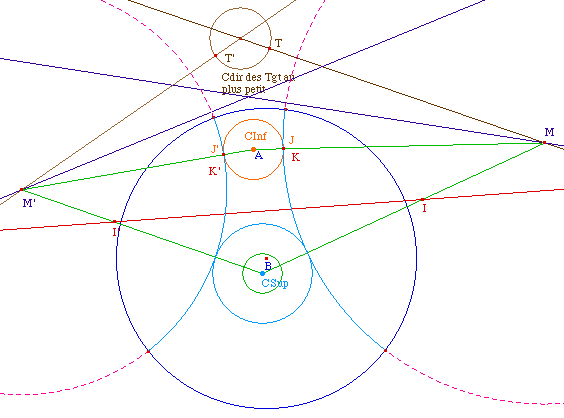
Nous sommes toujours dans le cas des tangentes communes "extérieures" - de même type, mais quand les deux cercles de base sont tangents intérieurement à la tangente commune (on remarquera que dans le cas euclidien, on est à la frontière de cette distinction entre les deux).

Le point M' est centre d'une telle tangente, car le segment [M' CSup] ne coupe pas la médiatrice, alors que le segment [M' CInf] la coupe en U. On construit alors V, comme J ci-dessus, puis on conditionne le symétrique de V par rapport à CInf à l'existence de U, ce qui donne un point W.

Le cercle de centre M' passant par W - quand il existe - est le support d'une tangente commune aux deux cercles telle que les cercles lui soient intérieurs.

Il faut aussi faire la construction pour M.
HCrcl27c.fig (figure intérmédiaire du cas "contacts de mêmes types" achevé)

 

e - Traitement du cas "Ext-int" (tangentes intérieures)

De la même manire, la macro Deux contacts autre nature ( ContAT.mac - de la page BFSolP02.html ) appliquée à CInf, C et C" cette fois (vert foncé ci-dessous), renvoie les points du cercle C qui générent les points communs à la conique de foyer CInf de cercle directeur C et celle de foyer CInf de cercle directeur C". Cette macro donne deux points S et S'. La droite passant par S et le centre de C coupe la médiatrice de [S CInf] en P.

 

Ce point P est centre d'une tangente commune intérieure (type "Ext-Int") ssi il est du même côté que Cinf de l'hyperbole, c'est-à-dire de l'autre côté que CSuf par rapport à la médiatrice de [Cinf CSup] pour avoir un contact extérieur sur le plus grand cercle et intérieur sur le plus petit.

On construit alors L intersection de la médiatrice et de [P CSup]. On construit sous X, intersection du cercle bleu clair (le plus grand des deux) avec [P CSup], un point Y conditionné à l'existence de L.

Alors, quand il existe, le cercle de centre P passant par Y est support d'une tangente commune aux deux cercles, avec des contacts de nature différente, le contact étant extérieur sur le plus grand des deux cercles.

On fait de même pour S', et on traite à nouveau les deux cas où le contact extérieur a lieu sur le plus petit cercle.

HCrcl27d.fig (ci-contre)

HCrcl27e.fig (figure finale du cas des contacts de type différents)

Il est clair que certains cas particuliers ne sont pas traités, en particulier celui où l'un des cercles passe par l'origine du cercle de Poincaré, car dans ce cas la conique des centres des tangentes n'est pas bifocale puisque, nous l'avons vu à la page précédente, c'est une parabole.

   HCrcl24.fig (figure finale par macro) ou THComExt.mac ou THComInt.mac

 

 

 [III.5.a. Tangente à un cercle] [III.5.b. Lieu des centres des tangentes à un cercle] 

[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 - Médiatrice, milieu ...] [III.4 - Horocycles] [III.6 - Premières utilisations]

[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]

[Retour aux GNE]

 

Menu général