IV.1.a - Bissectrices - cercle inscrit

[IV.1.b - Cercles exinscrits]

Rappels succints sur les résultats utilisés dans ce chapitre 

On sait que le modèle hyperbolique de Poicaré est conforme, c'est-à-dire que ses angles hyperboliques sont les angles euclidiens de ses tangentes. On a vu également dans la présentation axiomatique de Jacqueline Lelong Ferrand que les bissectrices sont les axes de symétries des droites, et donc qu'en géométrie hyperbolique un triangle isocèle a ses côtés et ses angles égaux.

Par ailleurs, on sait que dans le modèle hyperbolique, la somme des angles d'un triangle est toujours inférieure à deux droits. On appelle défaut angulaire la différence à Pi. Il sera, là encore, intéressant de voir comment sont mises en défaut nos habitudes euclidiennes liées la somme des angles d'un triangle.

On a vu aussi que les isométries ayant un point fixe sont les rotations, composées de deux symétries orthogonales d'axes sécants. Enfin, aprés avoir choisi une définition des polygones réguliers et construit quelques uns, ce chapitre se terminera par l'illustration d'un théorème sur les pavages qui montre que le plan hyperbolique est infiniment plus riche que le plan euclidien pour ce qui est de cette question.  

Bissectrice intérieure de l'angle AOB

a - Construction

On note I et J les centres des droites (AO) et (OB), donnés par la macro droite hyperbolique, puis on construit les tangentes euclidiennes à [IO] et [JO] en O.

HAngl01.fig ou BissIntH.mac (macro de base)

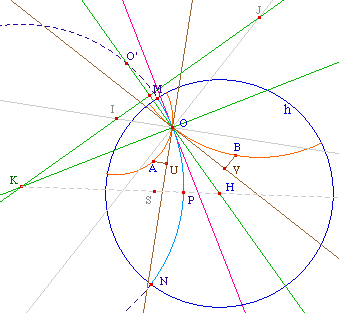
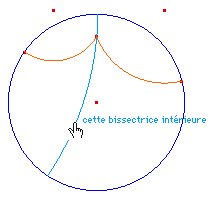
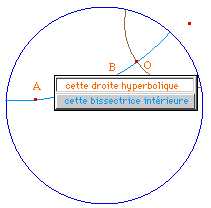
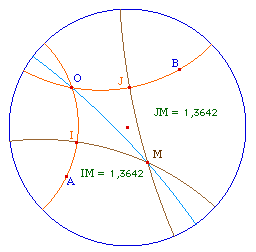
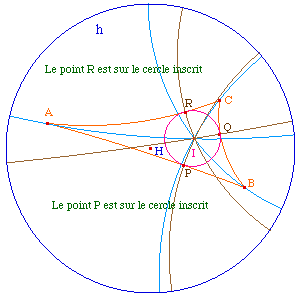
Pour prendre la bissectrice intérieure, il faut s'assurer de prendre des points de la tangente du secteur angulaire qui convient. Pour cela, il suffit de projeter A et B sur les tangentes en U et V. On trace ensuite la bissectrice euclidienne de UOV - droite rose ci-contre. De par la conformité du modèle, cette droite est tangente euclidienne à la bissectrice hyperbolique de AOB. Pour obtenir la bissectrice, on construit son centre K qui est sur la perpendiculaire à cette droite en O et sur la médiatrice de [OO'] où O' est l'inverse de O par rapport à l'horizon. Cette intersection n'existe pas si O est un point idéal, il faudra une construction particulière. En fait, cette dernière droite, par construction, est aussi la droite (IJ) car c'est la droite - euclidienne - lieu des centres des droites hyperboliques passant par O. On construit ainsi la bissectrice hyperbolique intérieure, en bleu clair ci-contre.

Quelques remarques à prendre en compte pour obtenir une figure robuste :

- Pour que la bissectrice d'un angle plat (ou d'un angle nul) existe, on ne prendra pas K sur la droite (IJ) - car alors I et J sont confondus - mais sur la médiatrice de [OO'].
- Si dessus on a choisi de prendre O non constitutif de l'arc "bissectrice", pour cela on a pris un autre point P de l'arc (ici intersection avec la demi-droite [KS), S étant milieu de M et N). C'est peut-être un luxe inutile.

 

b - Illustrations de la robustesse de la construction

Cas où l'un des points (ici les deux) définissant l'angle est un point idéal de l'horizon
Cas où A, O, B sont alignés. Ici O entre A et B : la bissectrice est confondue avec la perpendiculaire en O à (AB)	Cas où A, O, B sont alignés. Ici O extérieur à [AB] : la bissectrice est confondue avec la droite (AB)

Comme on l'a déjà souligné sur les tangentes, ces deux dernières illustrations montrent aussi la finesse d'affichage de Cabri :
les deux arcs sont définis de manière trés différente, ils se superposent au pixel prés.

c - Les points sont bien équidistants de (OA) et (OB)

d - Optimisation de la macro

Avant d'utiliser systèmatiquement une macro de bissectrice, il peut-être intéressant de l'optimiser. En effet, un coup d'oeil sur les fichiers produits montre que la macro de base ci-dessus construit 62 objets intermédiaires pour tracer la bissectrice, essentiellement autour de la construction des points I et J de la figure 1. En effet, si on donne comme objets initiaux en plus de A, O et B ces deux centres, le nombres d'objets intermédiaires tombe à 16, soit une économie de 46 objets. C'est la raison pour laquelle le tracé de segments ou droites hyperboliques renvoie systématiquement le centre : pour qu'il serve d'objets initiaux dans le traitement des bissectrices ici, et plus généralement des angles comme on le verra dans les pages suivantes. D'où une nouvelle macro bissectrice :

BissIntO.mac (O pour optimisée) d'objets initiaux A, O, B, le centre de (AO) - ou [AO], celui de (OB) et l'horizon. Le nom de la macro est bissectrice int. optimisée.

Bissectrice de l'angle nul (en un point idéal)

 

HAngl02b.fig ou BissNul.mac

Le cercle inscrit

L'argument de distance suffit à prouver que les bissectrices intérieures d'un triangle sont concourantes en un point centre d'un cercle inscrit au triangle. HAngl03.fig Rappel technique important : pour la construction du point I, il est essentiel de prendre l'intersection de deux bissectrices "à la volée" - c'est-à-dire en pointant le curseur à l'intersection et en cliquant. Ceci doit se faire SANS LE MENU AMBIGUITE qui automatiquement place Cabri dans la procédure d'intersection de deux objets - ce qu'il faut absolument éviter ici sous peine d'avoir des problèmes lors des changements d'orientation. En particulier, si les trois bissectrices sont déjà tracées, il faut en cacher une pour prendre l'intersection. Remarque : par curiosité, on peut vérifier que l'utilisation de la macro optimisée fait gagner 138 objets sur cette simple figure (208 objets au lieu de 346)

Les macros associées :

3BissOpt.mac : objets initiaux A, B, C, OAB, OBC, OAC et l'horizon. Objets finaux : les trois bissectrices et leur intersection. (84 objets intermédiaires) 3BissOpC.mac : idem, renvoie en plus le cercle inscrit. (112 objets intermédiaires) CInscOpt.mac : idem, renvoie seulement le cercle inscrit. (92 objets intermédiaires) TRBissCI.mac : objets initiaux : A, B, C, l'horizon. Objets finaux : le triangle, les trois bissectrices, le cercle inscrit. Renvoie aussi les 3 centres des côtés du triangle. (187 obj. intermédiaires) TRdBisCI.mac : objets initiaux : A, B, C, l'horizon. Objets finaux : les trois droites support du triangle, les trois bissectrices, le cercle inscrit. Renvoie aussi les 3 centres des droites-côtés du triangle.(198 objets intermédiaires)

Remarque : dans toutes les macros, le point de contact du cercle avec le côté [AB] est un point constituant du cercle inscrit.

Point de Gergonne hyperbolique

HAngl04a.fig (Vérification et prélude à Gergonne)

HAngl04b.fig Point de Gergonne hyperbolique

Il serait intéressant de chercher une preuve de l'existence du point de Gergonne dans le contexte hyperbolique, de préférence avec l'axiomatique de Bachmann, car nous verrons que ce point existe aussi dans le modèle elliptique. Rappelons que dans le cas euclidien, les preuves sont souvent proposées dans un contexte de calcul barycentrique. Ici, il faut se placer dans une perspective uniquement métrique.

[IV.1.b - Cercles exinscrits]

Menu général