|
JML rentrant dans l'amphi pour
sa conférence sur
l'exploration des géométries hyperbolique et
elliptique,
surpris par le photographe Serge Cecconi
|
Présentation du
chapitre
Le modèle hyperbolique est d'abord un exemple de
géométrie métrique. Ainsi, par cercle
de centre O passant par A, on entend la ligne de niveau des
points M tels que OM = OA. Remarquons tout d'abord que
certaines équivalence euclidiennes ne fonctionnent
plus. Ainsi le cercle de diamètre [AB] comme
courbe orthoptique du segment [AB] - la fameuse
orthogonalité de (MA) et (MB) - n'est pas
valable dans les géométries non euclidiennes
car nous avons déjà vu que ce critère
est équivalent à l'axiome d'Euclide. Il faut
donc se méfier de nos réflexes
géométriques usuels, c'est d'ailleurs
l'intérêt de ces explorations.
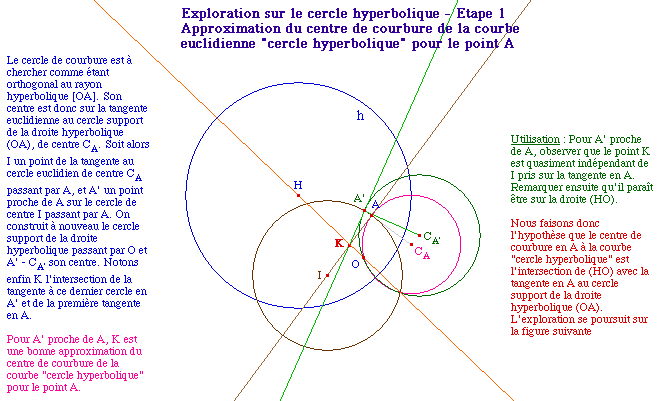
Dans cette page, nous reprenons la
merveilleuse introduction expérimentale de Jean Marie
Laborde. Cette présentation est d'autant plus
fantastique qu'elle se fait AVANT d'introduire l'expression
de la distance dans ce modèle. Dans la page suivante,
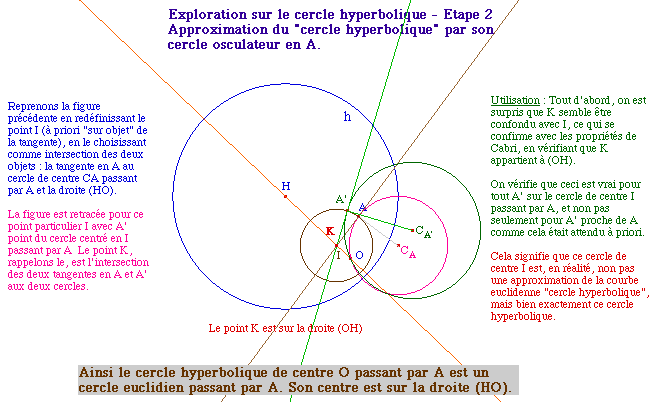
nous confirmerons - toujours selon une démarche de
simulation - que la construction proposée aboutit
bien à une ligne de niveau constante. Que ceux qu'une
preuve mathématique rassure ... le soit ... tout ceci
est démontré dans la partie VII des
compléments.
La réalisation des cercles
hyperboliques permettra ensuite dans les pages suivantes de
construire le milieu, la médiatrice et les
symétries associées, les symétries
centrales et orthogonales.
|