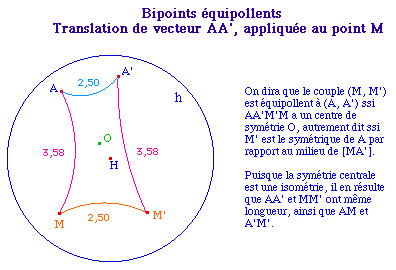
![]() TransO1.fig et macro
translaté Trans1pt.mac
utilisée ci-dessous
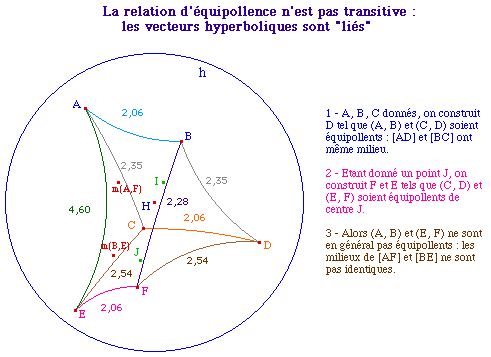
TransO1.fig et macro
translaté Trans1pt.mac
utilisée ci-dessous
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
[Retour aux GNE] [Menu général]

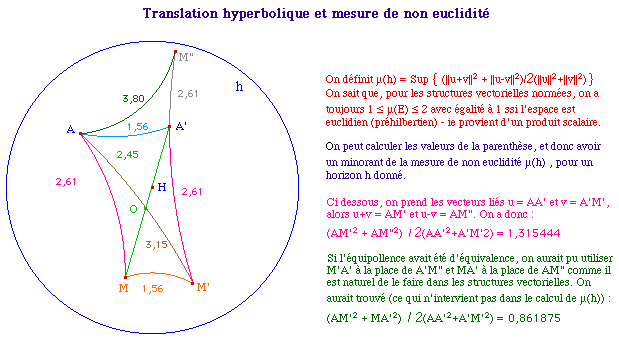
![]() TransO1.fig et macro
translaté Trans1pt.mac
utilisée ci-dessous
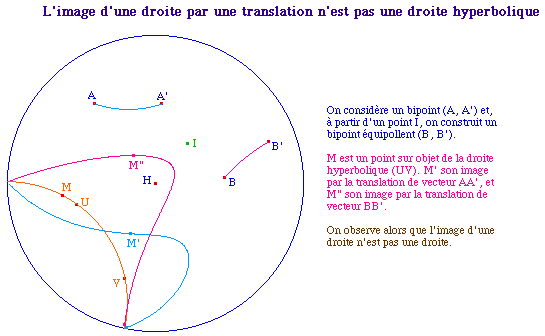
TransO1.fig et macro
translaté Trans1pt.mac
utilisée ci-dessous


![]() TransO4.fig (PC) ou TransO4M.fig
(Mac)
TransO4.fig (PC) ou TransO4M.fig
(Mac)
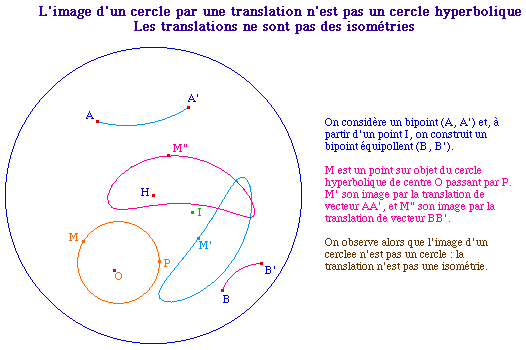
|
|
AnalyseSoit [CD] une solution et I le centre de symétrie de ABDC. Comme la symétrie est une isométrie, le cercle de départ, dans la symétrie de centre I est un cercle de même rayon, passant par A et B. Donc le symétrique de son centre est l'une des deux intersections U et V de la médiatrice de [AB] avec le cercle de centre B et de rayon OI.SynthèseSoient U et V les points indiqués ci-dessus, quand ils existent. Alors les milieux J de [OU] et Kde [OV] sont les centres de symétrie cherchés. Il suffit de construire les symétriques de A et B par rapport à I et J. Par construction on a des parallélogrammes et, toujours par construction, les points sont bien sur le cercle de départ.
|
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]