III.6.b - Non existence des homothéties

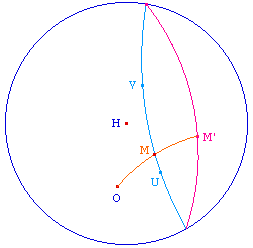
La situation précédente illustre aussi clairement que la composée de deux symétries centrales n'est pas une translation, ce que l'on sait puisque c'est une isométrie, ce qui n'est pas le cas de la translation.

Or, la composée de deux symétries centrales de centre A et B n'est rien d'autre que la composée de deux symétries orthogonales, les axes étant les perpendiculaires à (AB) en A et B.

Et il est alors intéressant de se rappeler ici qu'un axiome équivalent à celui d'Euclide est la distance constante entre deux droites sans point commun : la "distance" entre ces deux droites n'étant pas constante, directement lié au fait que la composée n'est pas une translation.

Soit maintenant V l'image de M dans la symétrie orthogonale d'axe passant par A. Le triangle MVM' admet les deux droites orthogonales à (AB) en A et B comme médiatrices. Or on a vu que les médiatrices d'un triangle forment un faisceau (droites concourantes ou ayant une perpendiculaire commune). Il en résulte que la médiatrice de [MM'] est aussi perpendiculaire à (AB). Autrement dit, la médiatrice de [MM'] est la perpendiculaire commune à (MM') et (AB).

Propriété : ABC un triangle, I, J, K les milieux de [AB], [AC], [BC]. Alors la perpendiculaire commune à (IJ) et (BC) est la médiatrice de [BC].

Homok2b.fig (PC) ou Homok2bM.fig (Mac)

L'image d'une droite est un arc de cercle dont le centre est sur la droite passant par le centre de la droite hyperbolique et celui de l'horizon.