Modèle hyperbolique de Poincaré
III. Cercle et distance

III.5.a - Tangentes à un cercle

[III.5.b. Lieu des centres des tangentes] [III.5.c. Tangentes communes à deux cercles]

[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 Médiatrice, milieu ...] [III.4 - Horocycles] [III.6 - Premières utilisations]

[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]

[Retour aux GNE] [Menu général]

Dans la page sur les horocycles, on a rappelé que les rayons étaient orthogonaux au cercle hyperbolique. Cela donne tout de suite la construction des tangentes en un point du cercle. On va donc s'intéresser plutôt aux tangentes issues d'un point.

Pour réaliser les figures ci-dessous, vous aurez besoin des macros CercleH.mac (cercle hyperbolique) DrtHypG.mac (droite hyperbolique), CtrHCrcl.mac (centre hyperbolique d'un cercle euclidien) et PerpHyp1.mac (perpendiculaire à une droite) mais aussi CnkFCdir.mac (Conique par foyer et cercle directeur).

Tangente en un point d'un cercle

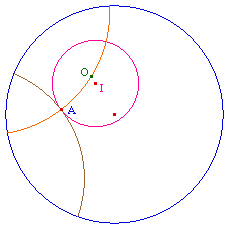Etant donné un cercle euclidien, inclu dans le disque de Poincaré, on construit son centre hyerbolique O. Par un point A du cercle, on trace la droite hyperbolique (OA).La tangente hyperbolique au cercle est la perpendiculaire en A à (OA).

HCrcl19.fig ou la macro TangSurC.mac

On notera que si le cercle euclidien n'est pas entièrement inclus dans l'horizon, le point O n'existe pas, la construction disparaît.

La page suivante étudie le lieu des centres de ces tangentes, dans l'optique de construire les tangentes communes à deux cercles.

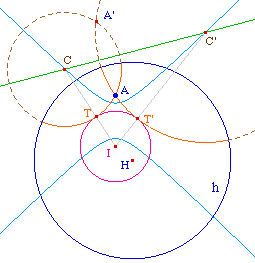Tangente en un point extérieur à un cercle

On considère un cercle de centre euclidien I, de rayon euclidien R, et un point A du plan hyperbolique, extérieur au cercle. Si on appelle T le point de contact d'une tangente hyperbolique au cercle passant par A, cette tangente aura son centre - euclidien - C tel que |CA - CI| = R. Ce centre est donc sur ll'hyperbole de foyer A et de cercle directeur le cercle de centre I. C'est une hyperbole car par hypothèse A est extérieur au cercle. On la trace par la macro CnkFCdir.mac.

Par ailleurs puisque la tangente cherchée est aussi une droite hyperbolique, son centre est également sur la médiatrice de A et de son inverse A' par rapport à l'horizon.

L'intersection de la droite et de l'hyperbole donne deux points C et C'. Les tangentes hyperboliques cherchées sont les traces sur le disque de Poincaré des cercles centrés en ces points, passant par I.

HCrcl20a.fig ou TangExtC.mac

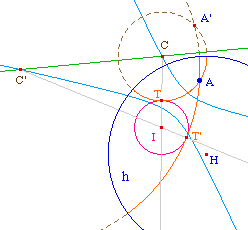On remarquera que la médiatrice de [AA'] peut couper l'hyperbole sur une seule branche ou sur deux branches. Les tangentes peuvent donc être toutes deux extérieures ou l'une extérieure l'autre intérieure.

Il en résulte que les points de contact T et T' sont les intersections des demi-droites d'origine C et C' passant par I avec les tangentes.

On notera aussi - ci dessous - que la médiatrice de [AA'] peut ne pas couper l'hyperbole ...

HCrcl20b.fig

[III.5.b. Lieu des centres des tangentes] [III.5.c. Tangentes communes à deux cercles]

[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 Médiatrice, milieu ...] [III.4 - Horocycles] [III.6 - Premières utilisations]

[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]

[Retour aux GNE]