III.5.b - Lieu des centres des tangentes à un cercle

[III.5.a. Tangente à un cercle] [III.5.c. Tangentes communes à deux cercles] 

Pour pouvoir construire les tangentes communes à deux cercles, une piste est de s'intéresser au lieu des centres des tangentes à un cercle : le centre des tangentes communes n'est rien d'autre que l'intersection de deux tels lieux.

Précisons toutefois que les résultats suivant - du moins pour l'auteur de ces pages - sont essentiellement empiriques : ce sont des résultats issus de l'expérimentation avec Cabri. abraCAdaBRI est donc intéressé par la publications de preuves géométriques proposées par les lecteurs : ce sont probablement de simples exercices d'utilisation des propriétés de l'inversion. Le détail de ces résultats est aussi proposé pour orienter des pistes de réflexion.

Le lieu des centres est une conique

Pour expérimenter ce résultat, on peut tracer le lieu des centres, puis construire une conique passant par 5 points "sur objet" de ce lieu, et vérifier ce que Cabri répond en terme d'appartenance à la conique pour un point courant du lieu. Voyons trois illustrations :

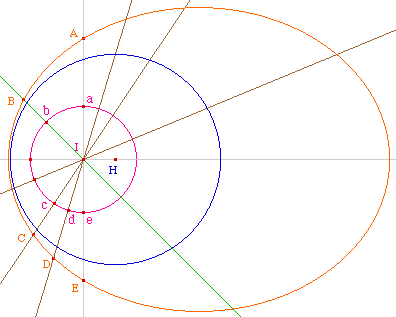
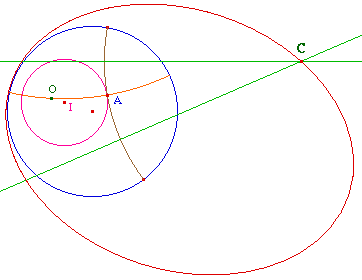
On reprend la figure HCrcl19. Pour mieux matérialiser le centre C de la tangentes, on a tracé les médiatrices des points constitutifs de l'arc "tangente".   HCrcl21a.fig   Le fait d'avoir laissé apparaître le centre euclidien laisse rèveur quant à l'un des foyers ... serait-ce possible que ??? ;-)

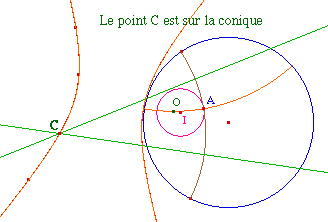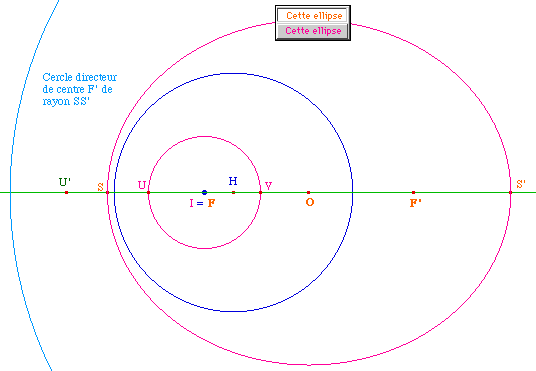
On le vérifie en construisant la conique passant par 5 points sur le lieu. En conservant l'ellipse, C est toujours sur la conique. Lors du passage à l'hyperbole, Cabri répond parfois que C n'est pas sur la conique HCrcl21b.fig Ce qui incite à construire la conique à partir de 5 points, construit à partir des données, sur le cercle de départ. Mais avant de construire effectivement la conique, testons le passage de l'ellipse à l'hyperbole ....

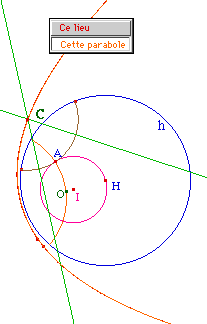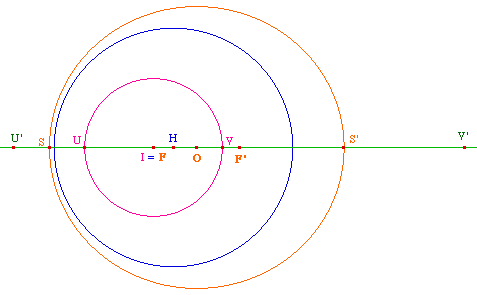
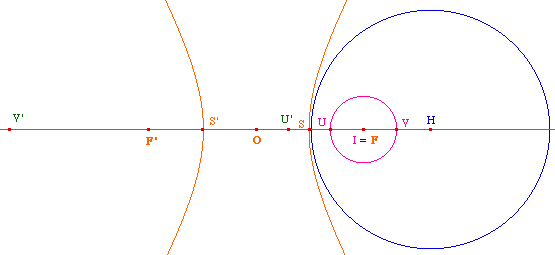
La manipulation de la figure précédente laisse envisager que la conique est une ellipse quand le centre de l'horizon est à l'intérieur du cercle sur lequel on travaille, et que c'est une hyperbole quand il est à l'extérieur. Et quand le cercle euclidien passe par le centre de l'horizon ? Il convient de refaire la figure (sauf si le cercle de départ est défini par 2 points) HCrcl21c.fig (nouvelle figure) Cabri confirme bien que quand le cercle passe par l'horizon on est à la frontière des deux cas généraux, la conique est dégénérée (au sens des quadriques) en la parabole. On retiendra le résultat empirique suivant : Le lieu des centres des tangentes à un cercle C est une conique. Plus précisément c'est une ellipse, une parabole ou une hyperbole selon que le centre de l'horizon soit à l'intérieur, sur ou à l'extérieur du cercle C.

Construction de la conique des centres des tangentes à un cercle

On peut transformer la figure 21b en une macro pour construire C à partir du cercle de A et de l'horizon. On applique cette macro à 5 points du cercle - construit par des bissectrices pour éviter les cas particuliers. L'expérience montre que cette macro présente des faiblesses : on prendra l'habitude de l'appliquer à une ellipse (H dans le cercle) et modifier le cercle comme on le souhaite ensuite : parfois dans le cas de l'hyperbole, la conique ne se construit pas. Nous allons donc améliorer cela en étudiant les propriétés de cette conique pour la tracer à partir de ses propres éléments.

 

HCrcl21d.fig ou la macro CnkCtTgt.mac

 

Propriétés de cette conique (obtenues empiriquement par Cabri)

Par l'utilisation de la macro FoyDir.mac on peut vérifier que le centre euclidien I du cercle est l'un des foyers de la conique - le foyer dans le cas de la parabole. La droite (IH) est clairement l'axe focal. En effet (IH) est un axe de symétrie par construction, or nous allons voir qu'il contient toujours un (cas particulier) ou deux points de la courbe, ce sera donc l'axe focal. Nous allons déterminer le sommet du côté de I, ce qui détermine entièrement la parabole, puis l'autre sommet et l'autre foyer dans le cas des coniques à centre, ce qui permet de construire le cercle directeur, et détermine ainsi la conique par ses éléments.

 

Si on note I le centre euclidien du cercle, H celui de l'horizon. La droite (IH) coupe le cercle en U et V (I entre U et H). Soient U' et V' les inverses de U et V par rapport à l'horizon. Alors, on a - pour les coniques à centre - le résultat symétrique suivant :

F, milieu de U et V est un foyer de la conique (c'est le point I, l'unique foyer si parabole)
F', milieu de U' et V' est l'autre foyer de la conique (point à l'infini si parabole)
S, le milieu de U et U' est un sommet (l'unique sommet si parabole)
S', le milieu de V et V' est l'autre sommet de la parabole.

HCrcl22.fig

On notera que le fait que S et S' soient des sommets est immédiat dans l'hypothèse que la courbe est une conique. En effet, sur la droite (HI), les centres des tangentes sont sur la médiatrices de [UU'] et de [VV']. Donc si U et V ne sont pas en H, cette médiatrice est une droite réelle qui coupe (HI) au milieu de U et U', et au milieu de V et V'.

Nous pouvons donc construire la conique à partir de son foyer F = I et de son cercle directeur le cercle de centre F' et de rayon SS', en utilisant la macro CnkFCdir.mac

 

On constate bien que les deux coniques coïncident parfaitement:
celle construite par 5 points étant point par point recouverte par celle construite par foyer et cercle directeur

Si on peut se permettre, ce point illustre aussi la qualité de l'affichage graphique de Cabri :
deux coniques identiques construites par des algoritmes différents donnent le même résultat au pixel près.

 

HCrcl23.fig ou CnkCTInt.mac (Int pour "intrinsèque")

 

Dans la suite, on utilisera cette seconde macro pour les constructions, en particulier pour les tangentes communes à deux cercles.

[III.5.a. Tangente à un cercle] [III.5.c. Tangentes communes à deux cercles] 

Menu général