[III.1. Approche expérimentale du cercle] [III.3 - Médiatrice, milieu ...] [III.4 - Horocycles] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
[Retour aux GNE] [Menu général]
 |
|
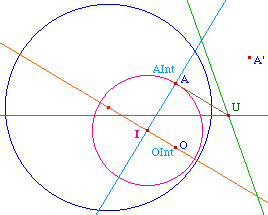 |
Il n'est pas nécessaire de construire le cercle support de la droite hyperbolique, son centre suffit, la construction devient alors celle- ci :
|
 |
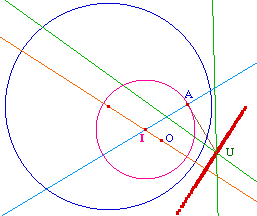
Deux limites à cette construction :
|
 |
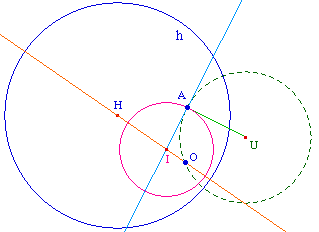
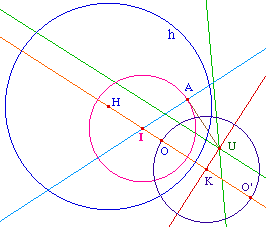
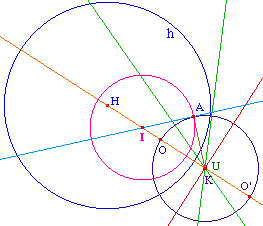
Jean Marie Laborde observe alors le lieu de U quand A se déplace dans le disque horizon : on l'obtient en faisant la trace de U et en déplaçant A manuellement.On commence à avoir maintenant un peu l'habitude pour "sentir" que cette droite n'est autre que la médiatrice de [OO'] où O' est l'inverse de O par rapport à l'horizon.On vérifie facilement que c'est vrai. Alors, en plaçant A - de manière perceptive - pour que U viennent en K (ci-dessous), on remarque que A vient sur ce cercle de diamètre [OO'].Cela signifie aussi que le cercle hyperbolique cherché est aussi le cercle centré sur (OH) orthogonal à ce cercle de diamètre [OO'], ou encore que I est sur la médiatrice [AA"] où A" est l'inverse de A par rapport à ce cercle |
 |
 |
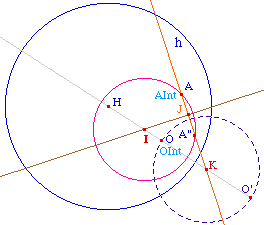 |
Aprés avoir construit OInt et AInt par la macro , on construit le cercle C de diamètre [OO'] où O' est l'inverse de OInt par rapport à l'horizon. On construit alors ensuite :
|
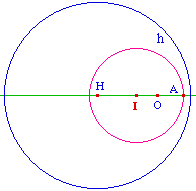 |
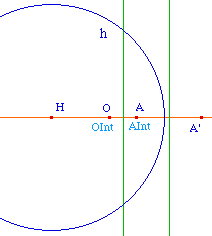
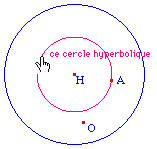
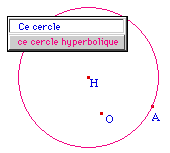
On vérifie que si H, O, et A sont alignés le cercle hyperbolique existe (bien ci-contre à gauche)De même, on peut construire le cercle hyperbolique de centre H passant par A (ci-contre à droite). Il est alors confondu avec le cenrcle euclidien de même centre. |
 |
 |
|
 |
 |
Pour faire la construction, on a besoin de la
macro
|
|
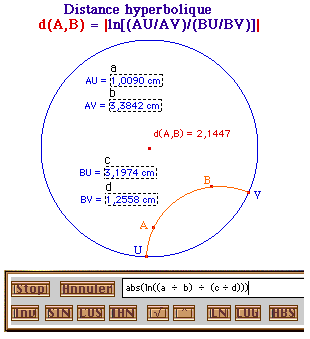
et vérification numérique |
[III.1. Approche expérimentale du cercle] [III.3 - Médiatrice, milieu ...] [III.4 - Horocycles] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
[Retour aux GNE] [Menu général]