CercleH.mac (cercle hyperbolique)
DrtHypG.mac (droite
hyperbolique), SegHyper.mac
(Segment hyperbolique) et DistHyp.mac
(Distance hyperbolique).[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.4 - Horocycles] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
[Retour aux GNE] [Menu général]
CercleH.mac (cercle hyperbolique)
DrtHypG.mac (droite
hyperbolique), SegHyper.mac
(Segment hyperbolique) et DistHyp.mac
(Distance hyperbolique).
|
|
|
|
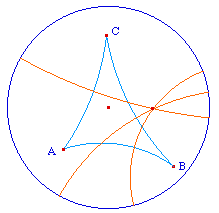
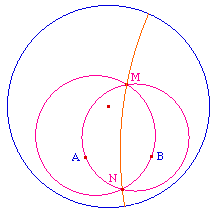
Les médiatrices sont concourantes ... |
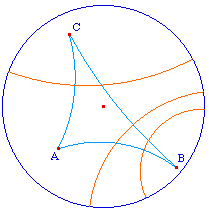
... ou parallèles |
HCrcl11.fig ou la macro MedTR3pt.mac
qui renvoie les trois médiatrices et leur intersection
éventuelle
 |
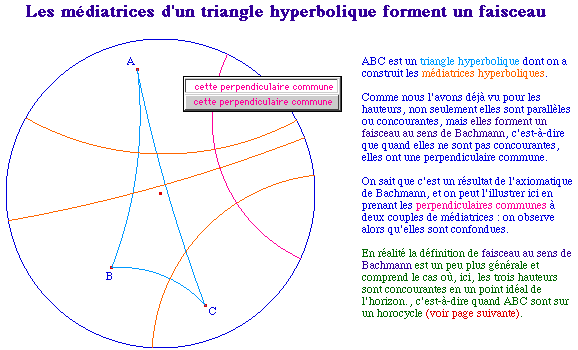
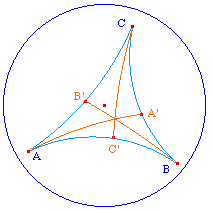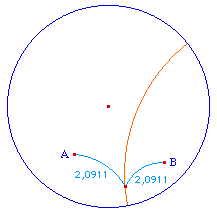
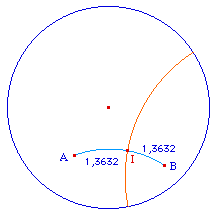
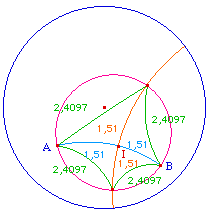
Par contre que les médianes soient concourantes est, selon le contexte, soit une "surprise hyperbolique", soit un résultat connu de la construction axiomatique de Bachmann.
|
|
|
Le symétrique de A par rapport est le point A' tel que O est milieu de A et A'. Pour cela, on trace la droite (AO) et le cercle de centre O passant par A.A' est alors l'autre point d'intersection du cercle et de la droite.Toutefois, dans l'implémentation dynamique de Cabri, il faut prendre quelques précaution pour éviter la situation ci-contre |
|
|
En effet quand la droite (AO) franchit le centre du cercle horizon, l'orientation change sur l'arc mais pas sur le cercle qui est toujours le même. Il convient donc d'adapter l'argument purement mathématique.On peut par exemple, comme ci-contre, prendrela droite passant par le centre euclidien du cercle hyperbolique et le centre - toujours euclidien - de la droite (AO). A' est alors le symétrique - euclidien - de A par rapport à cette droite. En effet, c'est un point du cercle et de la droite hyperbolique - donc un point commun, autre que A. C'est bien le point A' cherché.
|
 |
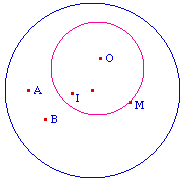Bien-sûr la symétrie centrale permet de construire l'équivalent hyperbolique du compas : soit I le milieu de [OB], et M le symétrique de A par rapport à I. Comme la symétrie centrale est une isométrie, on a d(O, M) : d(A, B). Et donc le cercle de centre O passant par M est le cercle de centre O et de rayon AB.
|
|
HCrcl14.fig ou la macro
SymAxeH.mac |
On fait de même pour la symétrie axiale. Comme on souhaite pouvoir l'appliquer aussi bien par rapport à un segment qu'à une droite, là encore, il faut prévoir quelques aménagement. On travaillera sur un segment [AB]. On peut commencer par prendre la perpendiculaire en M au segment ([AB]. On reconstruit ensuite le centre du cercle support à partir des trois points constituant l'arc de cercle.Pour prendre l'intersection O entre l'arc "droite orthogonale" passant par M et le cercle, prendre la précaution de cacher le segment [AB] car l'intersection DOIT se prendre dynamiquement, "à la volée" en pointant à l'intersection - ce qui n'est pas la même chose que faire "intersection de deux objets" comme déjà mentionné sur la page I.4.On termine comme ci-dessus, en prenant la droite passant par le centre I de la perpendiculaire et le centre euclidien J du cercle de centre O passant par M. On termine par le symétrique - euclidien - de M par rapport à cette droite. Le point M' est alors le symétrique orthogonal dans tous les cas de figure. |
 |
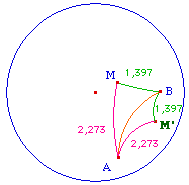En fait les symétries orthogonales de ce modèle du disque de Poincaré ne sont autre que les inversions par rapport au support de l'arc ou de la droite hyperbolique. La construction est donc plus élémentaire.Sur cette figure, M' est construit comme inverse de M par rapport au cercle bleu clair (l'arc suffit pour Cabri). On vérifie alors que les segments BM et BM' ont même longueur, ainsi que AM et AM' : autrement dit la droite (AB) est bien la médiatrice de M et M', ce qui est - aux points invariants prés sur l'axe, la définition de la symétrie orthogonale.
|
L'inversion comme symétrie orthogonale et l'axiomatique de Bachmann
Dans cette axiomatique - comme dans d'autres - le concept de réflexions et d'isométries remplace la congruence des axiomatiques de type Euclide-Hilbert : le groupe des isométries permettra d'écrire plus simplement - avec le vocabulaire de l'algèbre - certaines propriétés géométriques de base.
Le groupe d'axiomes "M3" sur les réflexions dans l'axiomatique de Bachmann est le suivant :
Toute droite d est l'axe d'au moins une réflexion
La composée de trois réflexions par rapport à trois droites ayant en commun un point ou une perpendiculaire est une réflexion par rapport à une droite.Voici deux illustrations, réalisées sur la même figure par des considérations de géométrie logique, qui résument la situation.
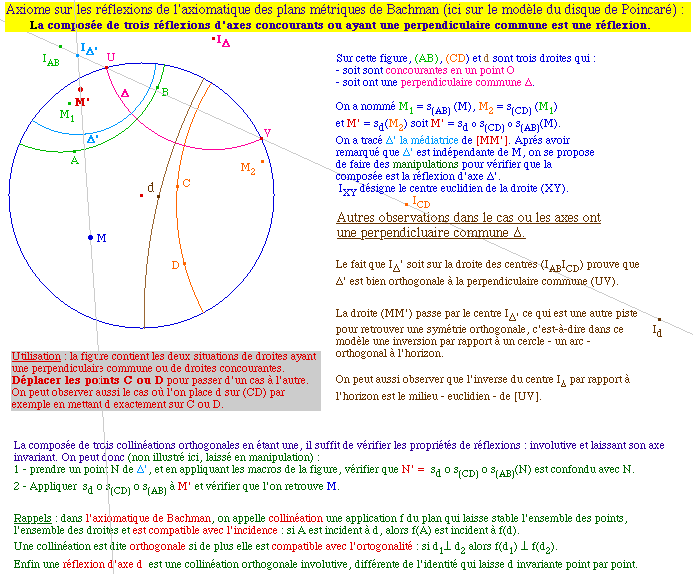
Voir la même figure dans le modèle de Klein-Beltrami
 |
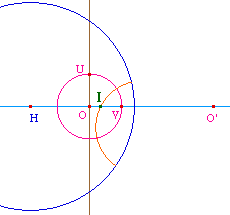Il sera utile, dans certains contextes, d'utiliser un cercle de base - on dira euclidien - dans le disque de Poincaré. Il est alors nécessaire de pouvoir préciser son centre hyperbolique.Soit - comme ci-contre - un cercle euclidien de centre O, strictement inclus dans le disque de Poincaré de centre H. Notons I son centre hyperbolique. On a vu que O est sur la droite des centres (HI). Donc I est sur la droite (HO). Pour des raisons de passage à l'infini quand O vient en H, on a préfère utiliser la droite (HO') où O' est l'inverse de O dans l'inversion par rapport à l'horizon. Soient U et V deux points du cercle euclidien, non alignés avec O. Alors le centre hyperbolique du cercle est l'intersection de (HO') avec la médiatrice hyperbolique de U et V.
|
[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.4 - Horocycles] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
Menu
général 
