1 - Présentation générale

A la suite des travaux de Klein, on appelle hyperbolique une géométrie de Lobatchevsky pour laquelle par un point il passe deux droites non sécantes et sans perpendiculaire commune à une droite donnée. Bachmann nomme cette situation "droites non connectables". D'autres axiomatiques sont possibles, plus directes quant à l'étude des propriétés métriques : nous présenterons plus loin celle de Jacqueline Lelong Ferrand (JLF) qui permet de présenter la "géométrie absolue" au sens de Bolyai, c'est-à-dire qui vérifie les quatre premiers axiomes d'Euclide : comme le fait remarquer JLF, la géométrie hyperbolique est à 80% ... euclidienne.

Les droites dans les trois modèles classiques | Les isométries en référence à l'axiomatique de Bachmann | Le contenu des pages "Poincaré" et "Klein-Beltrami"

Trois modèles plans de géométrie hyperbolique 

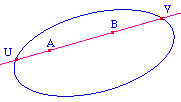
Historiquement, Cayley a d'abord montré que l'intérieur d'une conique - projective réelle -non dégénérée, munie de la distance d(A,B) = k.| ln[(AU/AV)/(BU/BV)] | est un modèle de géométrie hyperbolique dans lequel la droite (AB) est l'intersection de la droite euclidienne avec l'intérieur stricte de la conique. Cette page utilise la distance de Cayley

Modèle de Klein-Beltrami

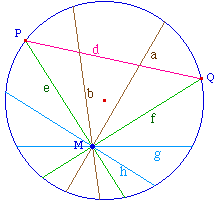
Suite à ses travaux sur la pseudo-sphère, Beltrami a proposé le modèle dit de "Klein-Beltrami" dans lequel la métrique est encore celle de Cayley (avec k = 1 par exemple) Les droites sont les cordes du cercle, privées de leurs extrémités. Parmi les droites du faisceau issu de M, on distingue Les droites sécantes à d (exemple a et b). Les droites non connectables à d (ex. e et f), celles que Lobachevsky appelle parallèles Les droites non sécantes à d : elles sont connectables sans point commun, et donc ont une perpendiculaire commune avec d (exemple g et h).

Modèle du disque de Poincaré

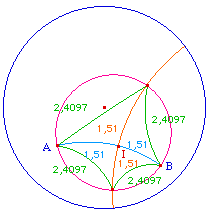
Dans ce modèle, les droites sont des arcs de cercle, orthogonaux au cercle horizon (la conique absolue de Cayley). Par rapport au précédent, ce modèle est conforme : les angles hyperboliques sont les angles euclidiens des droites. On passe facilement du modèle de Kein-Beltrami au modèle de Poincaré, par le passage sur une sphère en perspective cavalière. Des pages d'abraCAdaBRI sont consacrées à ce passage. Ci-contre, un carré hyperbolique

Modèle du demi-plan de Poincaré

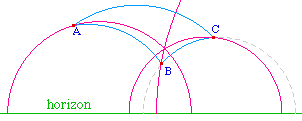
Dans le demi plan des nombres complexes de partie imaginaire positive, les droites sont les demi-cercles passant par deux points centrés sur l'axe réel (horizon) ou, s'il n'existe pas un tel cercle, la demidroite, dans le demi-plan voulu, passant par ces deux points (elle est alors orthogonale à l'horizon. Ce "ou exclusif" rend une Cabri-illustration moins simple (techniquement possible toutefois) puisque les droites ont deux formes différentes selon le contexte. C'est la raion pour laquelle on a privilégié la modèle précédent. Ci-contre : triangle ayant un orthocentre.

Les droites dans les trois modèles classiques | Les isométries en référence à l'axiomatique de Bachmann | Le contenu des pages "Poincaré" et "Klein-Beltrami"

Les isométries de ces modèles au regard de l'axiomatique de Bachmann

Dans cette axiomatique - comme dans d'autres - le concept de réflexions et d'isométries remplace la congruence des axiomatiques de type Euclide-Hilbert : le groupe des isométries permettra d'écrire plus simplement - avec le vocabulaire de l'algèbre - certaines propriétés géométriques de base.

Remarque : le demi-plan de Poincaré est le cas où le cercle horizon a son centre à l'infini : les symétries orthogonales sont les mêmes inversions que dans le cas du disque fini.

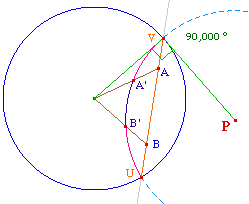
On notera que géométriquement, deux points fondamentaux sont communs aux deux modèles : le centre du cercle orthogonal à l'horizon passant par la droite hyperbolique de points idéaux U et V dans le modèle de Poincaré est le pôle de cette même droite idéale (UV) dans le modèle de Beltrami. Ainsi d'éventuelles propriétés sur les pôles de segments dans les figures du modèle de Klein-Beltrami seront donc aussitôt transférables en propriétés sur les centres des segments hyperboliques correspondants dans le modèle de Poincaré. Nous l'illustrerons sur les polygones réguliers. Cette simple remarque aide à mieux percevoir le passage d'un modèle à l'autre, et permet même de réaliser, par conjugaison, des constructions dans un modèle en utilisant leur homologue dans l'autre modèle. Le détail du passage effectif de [AB] dans le modèle de Beltrami à [A'B'] dans celui de Poincaré ainsi qu'un exemple de telle "conjugaison" sont proposés dans Passage d'un modèle à l'autre de l'introduction générale aux constructions hyperboliques.

Le groupe d'axiomes "M3" (3° groupe d'axiomes pour les plans métriques) sur les réflexions dans l'axiomatique de Bachmann est le suivant :

Toute droite d est l'axe d'au moins une réflexion
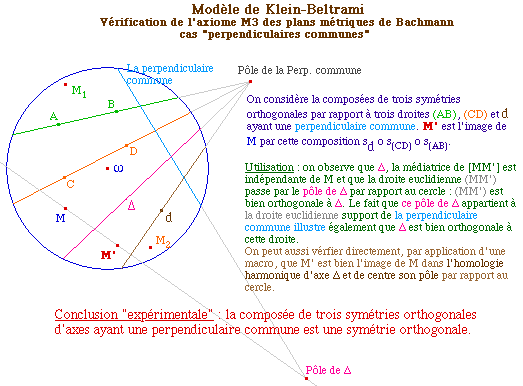
La composée de trois réflexions par rapport à trois droites ayant en commun un point ou une perpendiculaire est une réflexion par rapport à une droite.

La première assertion est vraie, trivialement, pour ces deux modèles, illustrons une vérification de la seconde propriété dans les deux modèles.

Remarque : Dans cette page d'introduction nous avons volontairement séparé les cas "concourantes" et "ayant une perpendiculaire commune", ce qui donne les 4 figures suivantes déjà riches d'information. Toutefois, les personnes déjà familiarisées avec ces modèles géométriques peuvent télécharger des figures plus synthètiques regroupant les deux cas dans chaque modèle disponilbes ici pour le modèle de Kein-Beltrami et là pour le disque de Poincaré.

Dans le modèle de Poincaré

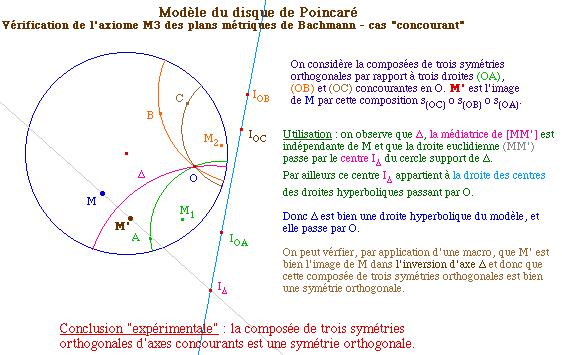
SOPBach1.fig

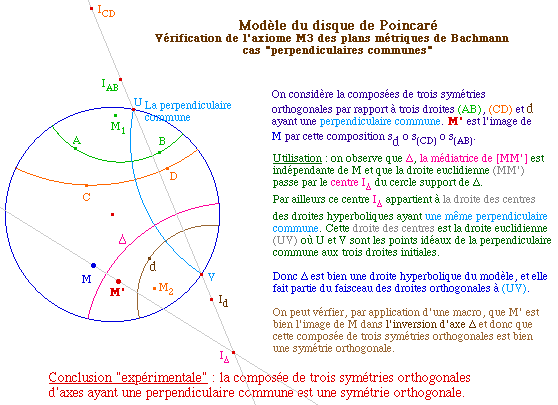
SOPBach2.fig

Dans le modèle de Klein-Beltrami

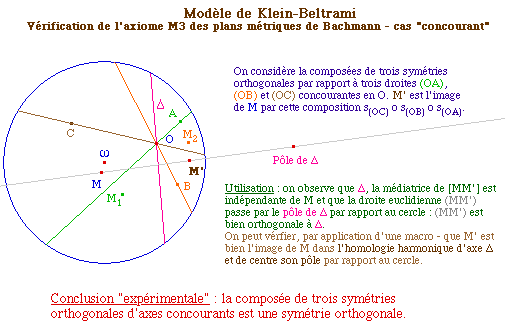
PropSym2.fig

 

PropSym3.fig

Les droites dans les trois modèles classiques | Les isométries en référence à l'axiomatique de Bachmann | Le contenu des pages "Poincaré" et "Klein-Beltrami"

Les pages sur le modèle du disque de Poincaré 

Approche constructive

La présentation proposée se veut volontairement expérimentale, dégagée le plus possible des considérations théoriques : c'est ainsi que l'on découvre, sur les pas de Jean Marie Laborde, la construction du cercle hyperbolique avant de connaître, à priori, la relation sur la distance. En dehors des points incontournables qui font la spécificité de la géométrie hyperbolique (perpendiculaire commune à deux droites, horocycle, faisceau des droites remarquables d'un triangle, etc), on a tenu à développer des Cabri-constructions qui sortent un peu de l'ordinaire de ce type de présentation, comme les tangentes à un cercle, et les tangentes communes à deux cercles ou encore les effets d'une translation ou d'une homothétie. Bien-sûr, on n'a pas résisté aux polygones réguliers, et une des illustrations Cabri qui en découle offre une approche perceptive saisissante de la vitesse en géométrie hyperbolique - et à l'occasion montre bien que la modèlisation de Cabri est structurellement celle d'un système affine euclidien. Elle se trouve en page d'acceuil de la version Java : abraJava.

Passages à la limite : les extensions du modèle

Dans les pages du dossier "disque de Poincaré", on observera que ce modèle se rapproche du modèle euclidien quand le rayon du cercle horizon tend vers l'infini et qu'il se rapproche du modèle hyperbolique du demi-plan quand le centre du cercle tend vers l'infini. Toutefois, parce que les constructions testent l'appartenance au disque, dans les constructions proposées, on ne peut donner la taille infinie au rayon ou renvoyer le centre à l'infini. Ce n'est pas une impossibilité de Cabri, mais seulement que ces figures utilisent une corde - un segment donc - du cercle, et qu'un segment ne peut devenir infini.

Aspect projectif idéal

Dehn a montré que tout plan métrique peut se plonger dans un plan projectif, dit "plan idéal" du plan métrique. Le comportement de Cabri rend compte de ce plan projectif pour la métrique euclidienne : avec Cabri, si deux droites sont séantes en I et qu'un troisème droite est construite passant par I, quand les deux droites initiales deviennent parallèles, la troisième continue d'exister et devient parallèle aux deux autres : autrement dit l'interface de Cabri a implémenté la notion de faisceau au sens de Bachmann pour la métrique euclidienne : quand les trois droites cessent d'être concourantes, elles ont une perpendiculaire commune et la troisième droite continue d'exister.

Nous nous efforcerons de faire de même dans le modèle de Poincaré. Des précisions et exemples de l'intérêt de telles constructions sont proposés à l'occasion. Dans un premier temps on notera que les figures Cabri réalisées pour ce modèle sont systèmatiquement valides "à l'infini", c'est-à-dire sur les points idéaux de l'horizon.

Les pages sur le modèle du disque de Klein-Beltrami 

Contrairement au modèle précédent, on a évité de tester les appartenances des points au disque :en pratique l'application de macros successives alourdit les figures de manière sensible. De même, certains commentaires à caractère théorique faits dans le premier modèle ne sont pas repris : les pages sont donc plus compactes, plus centrées sur les figures.

L'aspect des points à l'infini est plus facile à traiter, toutefois on a concervé des macros différentes pour les cercles et les horocycles tout en proposant une macro plus générale qui fonctionne dans les deux cas. D'une manière générale, les constructions utilisent aussi naturellement la formule de la distance pour, par exemple la construction du milieu ou du symétrique d'un point.

On trouvera développé des constructions qui ne sont pas dans le modèle précédent, comme la construction de Malfati. Enfin, une approche des coniques hyperobliques est proposée, avec une petite expérimentation Cabri pour déterminer quand la parabole hyperbolique de ce modèle est une parabole euclidienne.

Les droites dans les trois modèles classiques | Les isométries en référence à l'axiomatique de Bachmann | Le contenu des pages "Poincaré" et "Klein-Beltrami"

Menu général