[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]

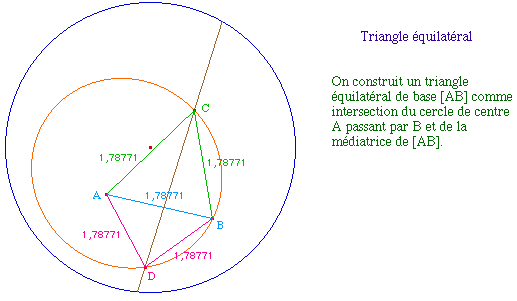
a - Cas d'un cercle
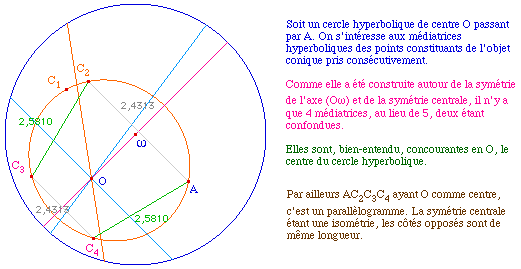
b - Réciproque
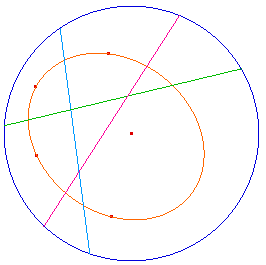
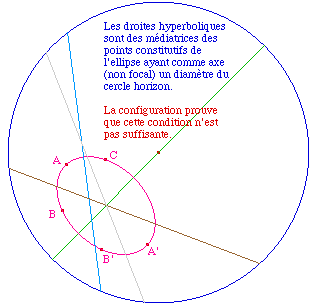
Mais toutes les ellipses ne sont pas des cercles hyperboliques. Ci-dessous on a pris trois médiatrices hyperboliques de 4 points constituants d'une ellipse : elles ne sont pas concourantes, c'est-à-dire qu'il n'y a pas de centre hyperbolique. Il serait donc intéressant de caractériser les ellipses "cercle hyperbolique".
 |
 |
3.a Construction "géométrique" | 3.b Construction "métrique" | 3.c Les horocycles | 3.d Premières utilisations
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]