BissI1KB.fig ou BissI1KB.mac
( à n'utiliser que pour comparer avec la suivante)
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]
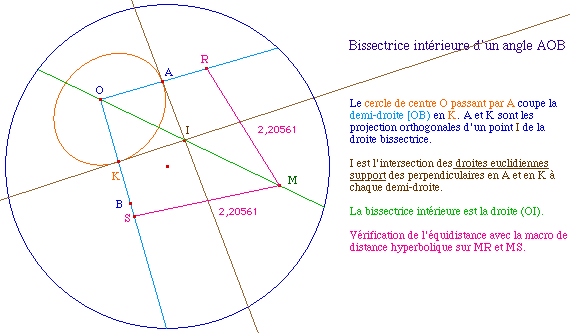
Le modèle de Poincaré est conforme : l'angle de deux droites hyperboliques est l'angle de ses tangentes euclidiennes et donc de même pour les bissectrices. Le modèle de Klein-Beltrami n'étant pas conforme, il est moins naturel s'appuyer sur des arguments euclidiens pour construire la bissectrice, même si nous utiliserons de tels arguments pour la mesure effective d'un angle. Mais en géométrie absolue, la bissectrice étant l'axe de symétrie d'un secteur angulaire, elle est aussi l'ensemble des points équidistants de deux droites, nous allons donc pouvoir baser notre construction sur cette propriété.
Première approche
BissI1KB.fig ou BissI1KB.mac
( à n'utiliser que pour comparer avec la suivante)
Cette figure utilise donc un cercle et deux perpendiculaires. Nous allons voir qu'on peut fortement la simplifier et même la généraliserApproche optimisée (proposée par Aldo Brigaglia et Grazia Indovina dans la revue italienne CABRIRRSAE n°15)
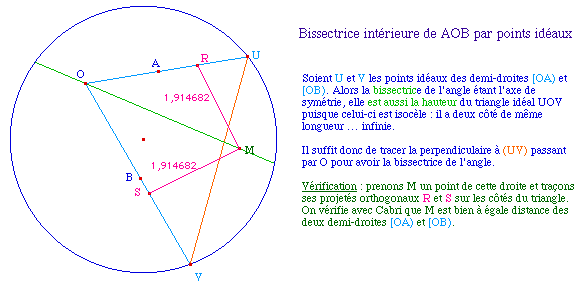
Dans la première version, il fallait 110 objets pour construire la bissectrice alors qu'avec cette utilisation de triangle idéal isocèle il suffit de 30 objets pour construire une bissectrice.On notera que la perpendiculaire pouvant être pris depuis un point idéal, la construction vaut aussi pour O idéal, c'est-à-dire pour la construction de la bissectrice d'un angle nul ... qui dans ce modèle peut être euclidiennement "grand".
|
|
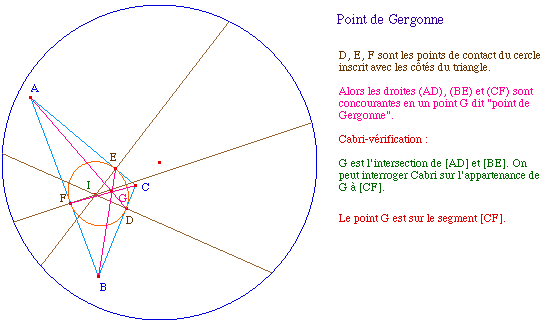
La bissectrice intérieure d'un angle étant l'ensemble des points équidistants de deux demi-droites, les trois bissectrices d'un triangle sont concourantes en un point centre d'un cercle inscrit au triangle.
|
|
|
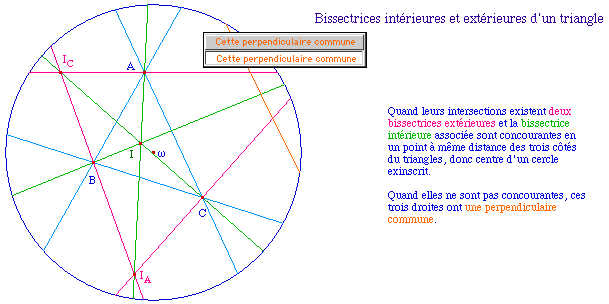
On fait de même pour la bissectrice extérieure, en utilisant un triangle idéal isocèle. A droite une illustration que l'on obtient bien la même droite en prenant l'une ou l'autre des demi-droite d'origine O. |
Elles forment un faisceau, au sens de Bachman :
4.b. Cercles exinscrits | 4.c.
Exemples d'applications | 4.d. La
construction de Malfati
4.e. Mesure des angles et construction
d'angles particuliers
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]
Menu général
