[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]
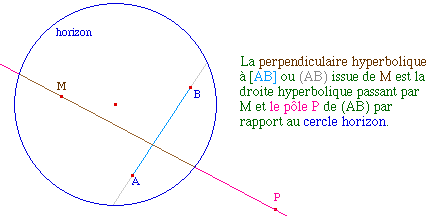
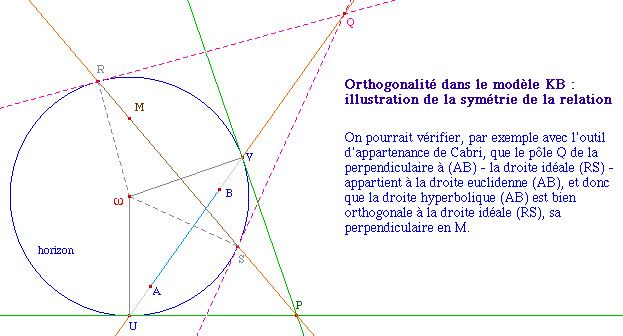
L'orthogonalité est bien une relation symétrique (on le sait, mais la figure est jolie ...)
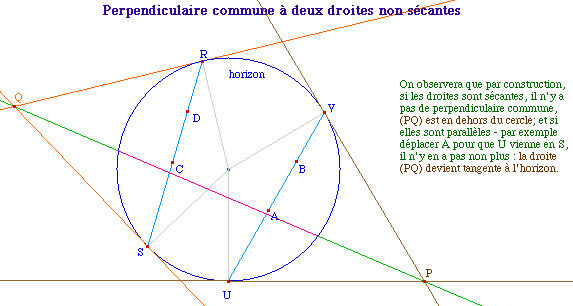
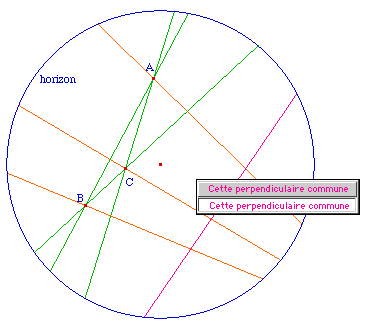
On sait que deux droites non sécantes et non parallèles (ie sans point idéal commun) admettent une perpendiculaire commune.
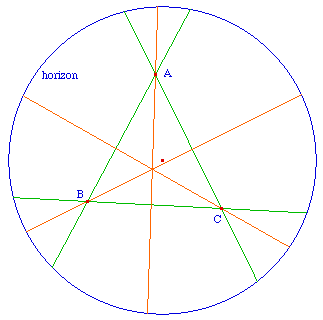
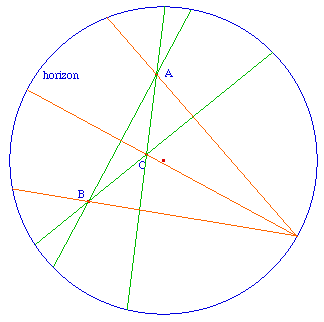
On sait que les trois cas sont possibles : elles peuvent être concourantes, non sécantes ou parallèles. Quand elles sont non sécantes, elles ont une perpendiculaire commune aux trois : on dit qu'elles sont en faisceau.
 |
 |
 |
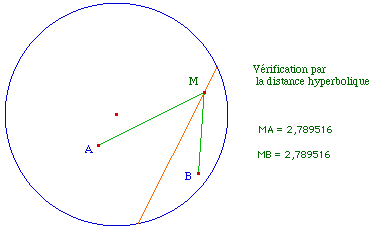On sait qu'en géométrie hyperbolique, la médiatrice de deux points A et B, ensemble des points équidistant de A et B, est la perpendiculaire à (AB) passant par le milieu. Comme nous avons à notre disposition une macro milieu et une macro perpendiculaire ... |
Les médiatrices d'un triangle forment aussi un faisceau
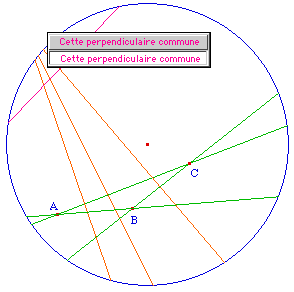
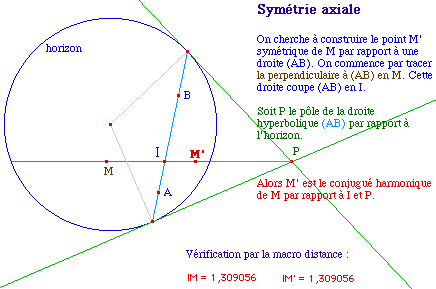
La symétrie axialeOn utilise une macro division harmonique
DivHarmo.mac déjà construite ici
La symétrie centrale
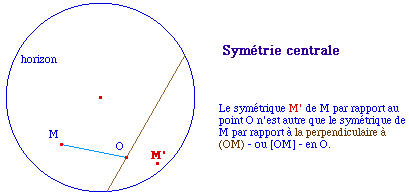
SymCGeKB.fig ou
SymCGeKB.mac (Ge pour
"géométrique")
Toutefois, on notera que cette construction est assez lourde (M' est le 46 ième objet de la macro). On peut économiser 10 objets en ayant une approche plus analytique, sur la base de la relation de la distance, comme pour la construction du milieu à la page d'introduction :
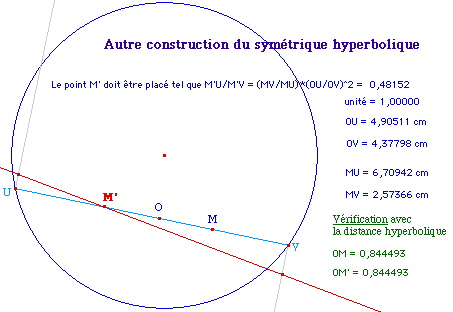
Comme cette symétrie interviendra dans la construction du cercle, c'est autant d'objets économisés pour la macro cercle hyperbolique.
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]
Menu général