[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]

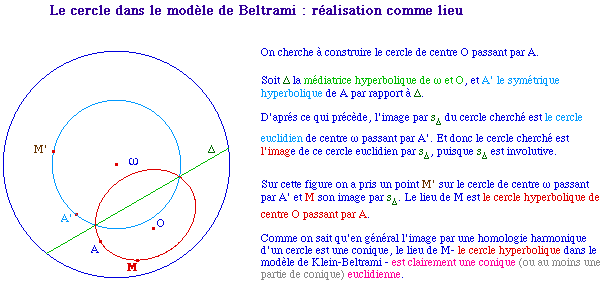
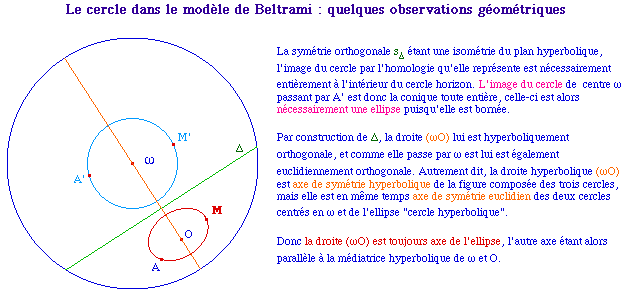
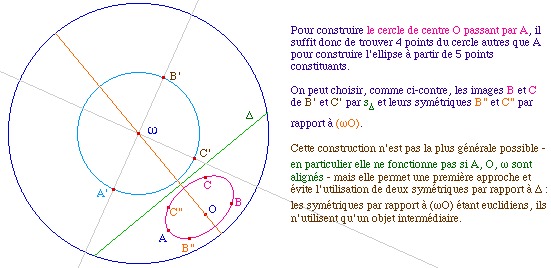
Toutefois cette construction présente au moins deux inconvénients :
- Elle n'est pas valide si O est au centre de l'horizon (ce point étant facilement améliorable en réalité)
- Elle utilise 136 objets intermédiaires, ce qui est beaucoup pour un cercle.
Dans la page suivante, par une approche à la fois plus métrique quant à l'obtention du lieu "cercle hyperbolique" tout en étant géométrique pour la construction effective de l'ellipse, nous proposons une construction qui aura moins de la moitié d'objets intermédiaires.
3.a Construction "géométrique" | 3.b Construction "métrique" | 3.c Les horocycles | 3.d Premières utilisations
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]