
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]
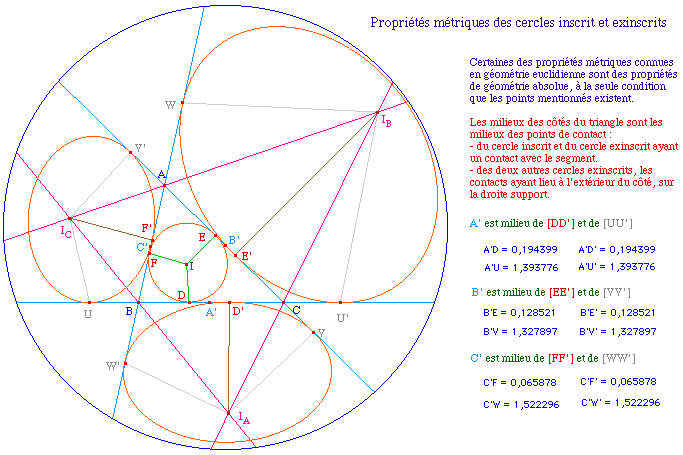
Pour une simple raison d'équidistance aux droites, si les bissectrices extérieures de deux sommets sont sécantes, elles sont concourantes avec la bissectrice intérieure du troisème sommet, et ce point de concourt, équidistant des trois droites, est centre d'un cercle tangent à ces trois droites : le cercle circonscrit opposé à l'angle de la bissectrice intérieure.


4.a. Les bissectrices | 4.c.
Exemples d'applications | 4.d. La
construction de Malfati
4.e. Mesure des angles et construction
d'angles particuliers
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]