Modèle hyperbolique de Klein
- Beltrami
KB.4.d - La construction de
Malfati
4.a. Bissectrices
intérieures | 4.b. Cercles
exinscrits | 4.c. Exemples
d'applications
4.e. Mesure des angles et construction
d'angles particuliers
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles] [Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
Le problème de Malfati (1803) consiste à construire
trois cercles intérieurs à un triangle, tangents entre
eux et aux côtés du triangle. À l'époque
on croyait avoir trouvé les trois plus grandes colonnes
pouvant être découpées dans un prisme de marbre,
mais en fait on s'est vite aperçu (1830) que ce n'est pas
nécessairement la solution maximale. Plus tard, Goldberg a
même montré, en 1967, que ce n'est jamais la solution
optimale à ce problème initial.
La construction de Malfati repose sur les bissectrices
intérieures d'un triangle et les symétries orthogonales
: rien que des considérations de géométrie
absolue. On peut donc la réaliser, telle quel, en
géométrie hyperbolique.
Etape 1
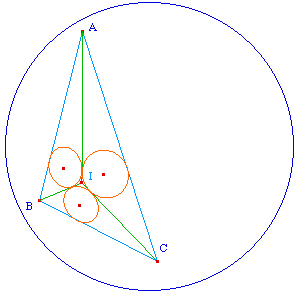
|
Soit I le centre du cercle inscrit au triangle ABC. On
construit les cercles inscrits aux triangles ABI, CBI et
CAI. Les droites (AI), (BI) et (CI), sont des tangentes
communes aux cercles pris deux à deux. Par
construction des cercles elles sont concourantes en I.
 Malfa1KB.fig
Malfa1KB.fig
Remarque :
pour la suite, on n'a pas besoin des cercles, mais seulement
des centres de ces cercles, on les a laissé pour
l'esthétique.
|
Etape 2
Les symétriques de ces tangentes communes par rapport
à la droite des centres des cercles concernés donnent
les autres tangentes communes des cercles pris deux à deux.
Elles sont elles aussi concourantes (propriété des
symétries orthogonales), ci dessous en Q.
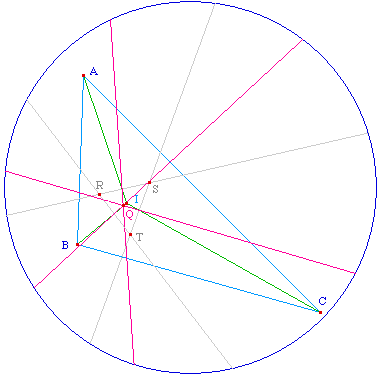
 Malfa2KB.fig
Malfa2KB.fig
Etape 3
La tangente commune aux cercles sans contact avec (AB) coupe (AB)
en M. On définit de même les points N et P.
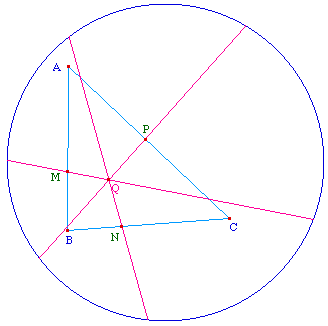
Alors les quadrilatères
AMQP, BNQM et CPQN sont des quadrilatères
circonscriptibles, c'est-à-dire qu'ils admettent chacun un
cercle inscrit : ce sont les cercles solutions.
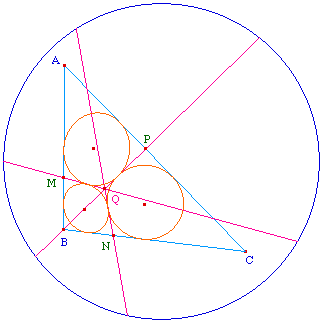
 Malfa3KB.fig
(46 Ko) et Malfa4KB.fig
(nettoyée)
Malfa3KB.fig
(46 Ko) et Malfa4KB.fig
(nettoyée)
Une propriété de la
construction de Malfati
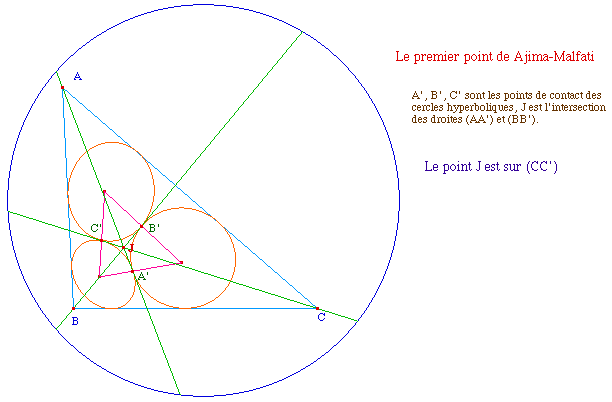
 Malfa5KB.fig
Malfa5KB.fig
Il existe un "second point" de Ajima : il est à
l'intersection de trois autres droites passant par A', B', C' et les
centres des cercles exinscrits à ABC correspondants, mais dans
ce modèle hyperbolique, la figure est assez lourde ...
Voir la
construction dans le modèle de Poincaré
(en CabriJava).
4.a. Bissectrices intérieures |
4.b. Cercles exinscrits | 4.c.
Exemples d'applications
4.e. Mesure des angles et construction
d'angles particuliers
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles] [Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
 Menu général
Menu général




