 |
modèles hyperboliques de Poincaré |
[Introduction] [Droites] [Cercles] [Angles] [Pavages] [Retour]
 |
modèles hyperboliques de Poincaré |
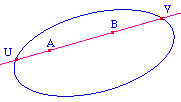 |
Historiquement, Cayley a d'abord montré que l'intérieur d'une conique - projective réelle -non dégénérée, munie de la distance
est un modèle de géométrie hyperbolique dans lequel la droite (AB) est l'intersection de la droite euclidienne avec l'intérieur stricte de la conique. |
Suite à ses travaux sur la pseudo-sphère, Beltrami a proposé le modèle dit de "Klein-Beltrami" dans lequel la métrique est encore celle de Cayley (avec k = 1 par exemple). Les droites sont les cordes du cercle, privées de leurs extrémités.
|
|
Ci-contre perpendiculaire communes à deux droites non sécantes. Manipulation possible : 1 - Observer tout d'abord que les droites sécantes n'ont pas de perpendiculaire commune. En géométrie hyperbolique, par un point il passe deux parallèles à une droite donnée. Dossier sur le modèle de Klein Beltrami (dans abraCAdaBRI) Droites et symétries en géométrie hyperbolique (dans abraCAdaBRI) |
C'est dans ce modèle que sont développés les constructions Cabri disponibles en applets CabriJava de ce dossier.
|
|
Les droites sont des arcs de cercle, orthogonaux au cercle horizon (la conique absolue de Cayley). Par rapport au précédent, ce modèle est conforme : les angles hyperboliques sont les angles euclidiens des droites, ce qui est très pratique ... ne serait-ce que pour l'orthogonalité. Ci-contre, la construction hyperbolique du problème de Malfati (ttrois cercles à l'intérieur d'un triangle, tangents entre eux et aux côtés du triangles) Remarque : si les cercles n'apparaissent pas, déplacer simplement un point, ils réapparaîtront. Voir aussi, dans abraCAdaBRI, des illustrations - et les figures Cabri - du passage du modèle de Kein-Beltrami au modèle de Poincaré, par le passage sur une sphère en perspective cavalière. Malfati dans le modèle de Klein Bletrami (dans abraCAdaBRI) |
Dans le demi plan des nombres complexes de partie imaginaire positive, les droites sont les demi-cercles passant par deux points centrés sur l'axe réel (horizon) ou, s'il n'existe pas un tel cercle, la demi-droite, dans le demi-plan voulu, passant par ces deux points (elle est alors orthogonale à l'horizon). Ce "ou exclusif" rend une Cabri-illustration moins simple (techniquement possible toutefois) puisque les droites ont deux formes différentes selon le contexte. C'est la raion pour laquelle on a privilégié la modèle précédent.
Ci-dessous : triangle (bleu) et ses trois hauteurs (roses). Il peut y avoir orthocentre ou non (déplacer par exemple B). Dans ce cas, en géométrie hyperbolique, les trois hauteurs ont une perpendiculaire commune (en orange quand elle existe).
Voici toutefois une barre de menu qui traite des cas
généraux et reste largement suffisante pour une
exploration![]() BardmPP.men
(95 Ko)
BardmPP.men
(95 Ko)
Pavages réguliers dans le demi-plan de Poincaré
La présentation proposée se veut volontairement expérimentale, dégagée le plus possible des considérations théoriques: c'est ainsi que l'on découvre, sur les pas de Jean Marie Laborde, la construction du cercle hyperbolique sans même connaître, à priori, la relation sur la distance. On trouvera, dans ces pages "CabriJava", l'essentiel des points incontournables qui font la spécificité de la géométrie hyperbolique : perpendiculaire commune à deux droites, horocycle, faisceau des droites remarquables d'un triangle, etc.
On a tenu à développer des Cabri-constructions qui sortent un peu de l'ordinaire de ce type de présentation, comme les tangentes à un cercle, et les tangentes communes à deux cercles. Mais ces constructions ne sont - pour le moment - disponibles que dans abraCAdaBRI (c'est-à-dire sans applet CabriJava, seulement avec des figures à télécharger et des illustrations), à cause de l'utilisation des coniques.
Bien-sûr, on n'a pas résisté aux polygones réguliers, et l'applet de la page d'accueil d'abraJava vous a proposé une approche saisissante de l'accélération en géométrie hyperbolique. On notera à l'occasion qu'elle montre aussi que la modèlisation de Cabri est structurellement celle d'un système affine euclidien.
Chacun pourra observer, en chargeant les figures des applets dans Cabri, que le modèle de Poincaré se rapproche du modèle euclidien quand le rayon du cercle horizon tend vers l'infini et qu'il se rapproche du modèle hyperbolique du demi-plan quand le centre du cercle tend vers l'infini.
Dehn a montré que tout plan métrique peut se plonger dans un plan projectif, dit "plan idéal" du plan métrique. Le comportement de Cabri rend compte de ce plan projectif pour la métrique euclidienne : avec Cabri, si deux droites sont sécantes en I et qu'un troisème droite est construite passant par I, quand les deux droites initiales deviennent parallèles, la troisième continue d'exister et devient parallèle aux deux autres : autrement dit l'interface de Cabri a implémenté la notion de faisceau au sens de Bachmann pour la métrique euclidienne : quand les trois droites cessent d'être concourantes, elles ont une perpendiculaire commune et la troisième droite continue d'exister.
Nous nous efforcerons de faire de même dans le modèle de Poincaré. Dans un premier temps on notera que les figures Cabri réalisées pour ce modèle sont systèmatiquement valides "à l'infini", c'est-à-dire sur les points idéaux de l'horizon.
Voir aussi (dans abraCAdaBRI) une histoire du V° postulat d'Euclide ou encore une illustration d'équivalences du V° postulat soit utilisées intuitivement, soit montrées explicitement.
|
 Retour sur
"abra-Java"
Retour sur
"abra-Java" |