|
|
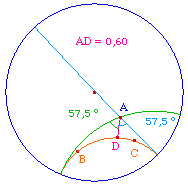
Par un point A passent trois types de droites :
L'angle Pi(x) = DAF = DAG est appelé angle de parallèlisme relativement à la distance x = AD. |
[Commentateurs] [Précurseurs] [Fondateurs] [Synthèses]
[Présentation chronologique] [Equivalences du V° postulat] [Le livre I d'Euclide]
|
|
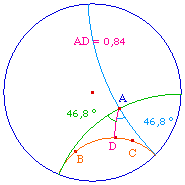
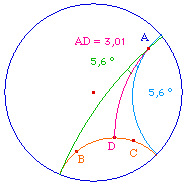
Par un point A passent trois types de droites :
L'angle Pi(x) = DAF = DAG est appelé angle de parallèlisme relativement à la distance x = AD. |
|
|
|||
|
|
|||
|
|
|||
de la fonction Pi |
La fonction Pi est donc une bijection décroissante de [0, ->[ sur ]0, Pi/2].
|
 |
 |
 |
|
|
|
|
|
|
sin A tan Pi(a) = Sin B tan Pi(b)
cos A cos Pi(b) cos Pi(c) = 1 - [sin Pi(b) qin Pi(c)] / sin Pi(a)
cot A sin C sin Pi(b) + cos C = cos Pi(b) / cos Pi(a)
cos A + cos Bcos C = sin B sin C / sin Pi(a)
1 - Sur une horosphère, surface obtenue dans la rotation d'un horocycle autour d'un de ses axes, si on fait jouer aux horocycles le rôle de droites, on obtient un modèle du plan euclidien, la trigonométrie des triangles sur ces surfaces étant la trigonométrie ordinaire.
2 - Si on suppose les côtés d'un triangle trés petits, les formules si dessus deviennent, en première approximation :
bsin A = a sin B ; a2 = b2 + c2 - 2bc cos A ; A + B + C = Pi
3 - Si on change a, b, c en ia, ib, ic dans les formules ci-dessus, on obtient les formules de trigonométrie sur une sphère de rayon k (ce qui avait d'ailleurs déjà été vu par Lambert) :
sin A sin b/k = sin B sin a/k
cos a/ k = cos b/k cos c/k + sin b/k sin c/k cos A
cot A sin C + cos C cos b/k = sin b/k cot a/k
cos A = cos a/k sin B sin C - cos B cos C
[Présentation chronologique] [Equivalences du V° postulat] [Le livre I d'Euclide]