II.4 - Perpendiculaire commune à deux droites

La page précédente contient en illustration deux résultats spécifiques à la géométrie hyperbolique :

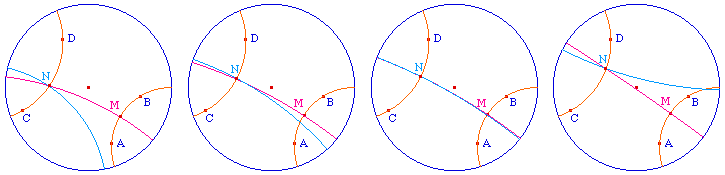
Etant donnés une droite d et un point A n'appartenant pas à d, il passe par A une infinité de droites sans point commun avec d mais ayant une perpendiculaire commune avec elle.

Etant donnés une droite d et un point A n'appartenant pas à d, il passe par A deux droites sans point commun et sans perpendiculaire commune avec d.

Nous nous proposons ici de construire une figure, spécifique plus généralement des géométries non euclidiennes, relative à l'inexistence de rectangles. Des manipulations sur les figures précédentes montrent que l'on ne peut pas construire de rectangle en géométrie hyperbolique, tout simplement parce qu'il est impossible de construire deux droites distinctes perpendiculaires à deux droites parallèles données : il n'y en a qu'une, c'est ce que nous allons construire.

Expérimentation sur l'existence et l'unicité de la perpendiculaire commune

Etant données deux droites hyperboliques (AB) et (CD) parallèles et un point M sur la première. Par M on mène la perpendiculaire à (AB). Elle coupe éventuellement (CD) en N. Par N on mène la perpendiculaire à (CD). Dans la structure euclidienne, les deux droites sont confondues. Ici, en déplaçant M, on observe qu'il n'existe qu'une position de M pour lesquelles les droites sont confondues, position que l'on peut approcher comme dans la troisième illustration. On parlera alors de la perpendiculaire commune à deux droites parallèles.

PerpCom1.fig (PC) ou PerpComM.fig (Mac)

 

Analyse et principe de la construction

La perpendiculaire commune (MN) au droites hyperboliques (AB) et (CD) est donc un cercle orthogonal à trois cercles : les deux droites et l'horizon. Cette construction est simple à réaliser, d'autant plus que l'un des cercles est toujours sécant aux deux autres. Voyons cela en quelques étapes :

Cercles orthogonaux à deux cercles donnés sécants

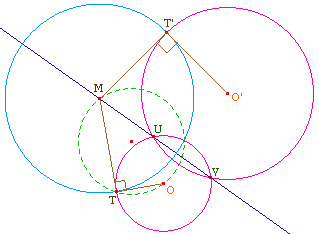Soient deux cercles C et C' sécants en U et V distincts. Un cercle orthogonal à ces cercles, de centre M, a ses tangentes aux deux cercles, MT et MT', égales à son rayon r, et donc M est nécessairement sur l'axe radical des deux cercles C et C' qui n'est autre que la droite (UV) dans ce cas où les cercles sont sécants. Réciproquement, pour tout point M de cet axe, en dehors du segment [UV], la construction usuelle de la tangente à l'un des cercles - comme ci-contre - permet de construire le cercle orthogonal à C et C' de centre M. PerpCom2.fig

Centre de la droite hyperbolique

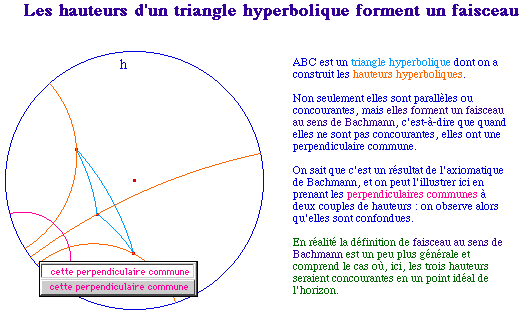
Puisque les droites hyperboliques coupent l'horizon, le centre de la perpendiculaire commune est nécessairement à l'intersection I des deux axes radicaux, le rayon étant construit pour avoir une tangente issue de I au troisième cercle qui est l'horizon.   PerpCom3.fig Sur cette figure générale d'analyse, les cercles de centre O et O' ne sont pas nécessairement orthogonaux à h : seul le cercle final est construit comme orthogonal à h. Son centre étant à l'intersection des deux axes radicaux, il est alors orthogonal aux deux autres.   Il reste toutefois à adapter cette construction si on veut n'avoir en objets initiaux de la macro que les deux droites hyperboliques et l'horizon.

 

Macro associée à cette construction

 

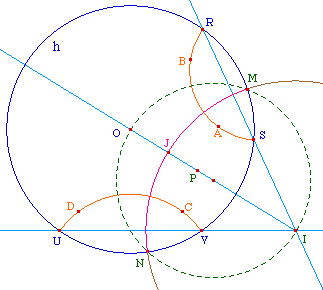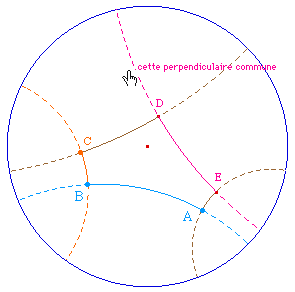
Comme les droites hyperboliques sont des arcs dont les points d'intersection avec l'horizon interviennent dans leur définition, il n'y a aucun problème particulier. Les droites (RS) et (UV) se coupent en I. Le cercle diamètre [OI] coupe l'horizon en M et N qui sont les extrémités de la droite hyperbolique cherchée. Il faut construire un point supplémentaire. On peut faire comme pour le cas des segments : ici P est le milieu de [MN] et la demi droite [IP) coupe le cercle support en J qui donne le point de l'arc.   PerpCom4.fig ou PerpComm.mac   Deux droites sécantes n'ont bien-sûr pas de perpendiculaires communes car l'intersection I des axes radicaux est à l'intérieur des cercles, il n'y a donc pas de tangentes au cercle horizon issues de I.

Comportements à l'infini

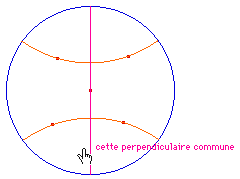
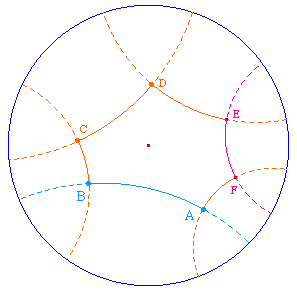
Si les droites (RS) et (UV) sont parallèles, la perpendiculaire commune est alors un diamètre du cercle horizon (centre à l'infini).

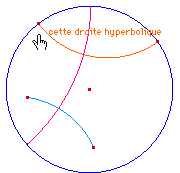
Perpendiculaire commune à un segment et à une droite définie par deux points idéaux.

Une première utilisation d'illustration

FaisHyp1.fig

 

Application fun : Pentagone et hexagone ayant respectivement 5 et 6 angles droits

 

Penta5D.fig

Hexa6D.fig

Polygones que l'on peut s'amuser à croiser en déplaçant les points de base A et B ou les points sur objet C et D.

 Ultérieurement, nous imposerons en plus aux polygones d'être réguliers ... mais ce sera une autre histoire ...

Menu général