Modèle hyperbolique de
Poincaré
II.Droites et orthogonalité
II.2 - Propriétés
d'incidence du plan hyperbolique
La page sera
complétée pour prendre en compte l'axiomatique de
Bachmann
[II.1. Droites et segments
hyperboliques] [II.3 -
Orthogonalité] [II.4 -
Premiers exemples d'utilisation]
[I. Introduction]
[III. Le cercle]
[IV. Les angles]
[V. Constructions]
[VI. Exercices]
[Retour aux GNE]
[Menu
général]
Il s'agit dans cette page, d'observer le
comportement de ce modèle hyperbolique sur les configurations
fondamentales quant aux structures éventuelles
sous-jacentes.
On sait que comme plan métrique, le
plan hyperbolique de Poincaré n'est ni projectif ni affine.
Toutefois, un plan métrique peut toujours être
plongé dans un plan plan projectif (plan idéal
associé). D'autre part le modèle de Klein du plan
hyperbolique est projectif. Les configurations fondamentales
d'incidence y sont vérifiées, elles le sont donc pour
ce modèle. Voyons en trois : celles de Désargues, de
Pappus, de Fano. C'est surtout l'occasion de premières
manipulations sur les droites hyperboliques.
Le plan hyperbolique et la configuration de
Désargue
Dans un contexte affine ou projectif, Artin
a montré que la configuration de Désargues est
équivalente à l'associativité de la
multiplication et donc à la structure de corps des nombres
construits par cette géométrie.
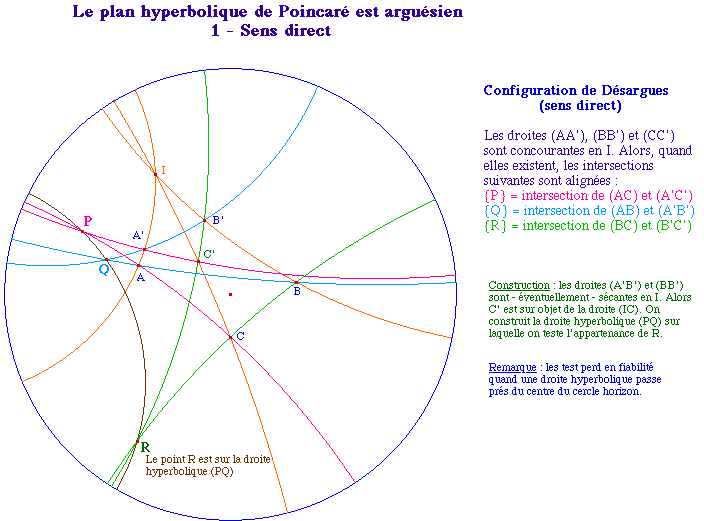
 Desarg1.fig (PC) ou Desarg1M.fig
(Mac)
Desarg1.fig (PC) ou Desarg1M.fig
(Mac)
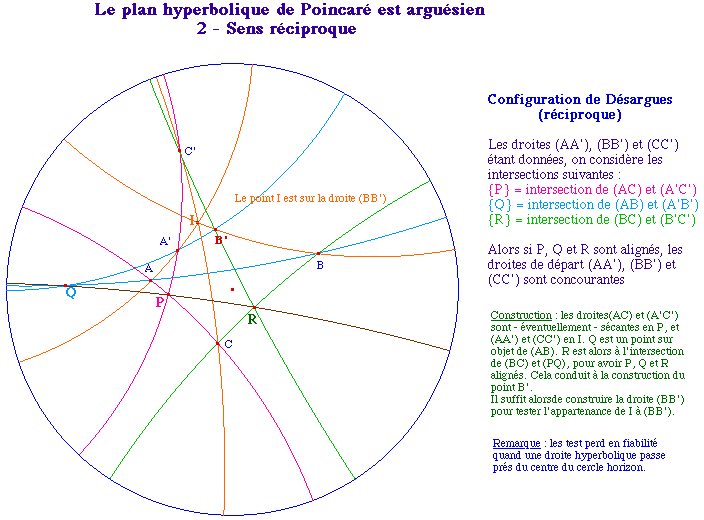
 Desarg2.fig (PC) ou Desarg2M.fig
(Mac)
Desarg2.fig (PC) ou Desarg2M.fig
(Mac)
Le plan hyperbolique et la configuration de
Pappus
Dans un plan arguésien, la
configuration de Pappus est équivalente à la
commutativité du corps des nombres.
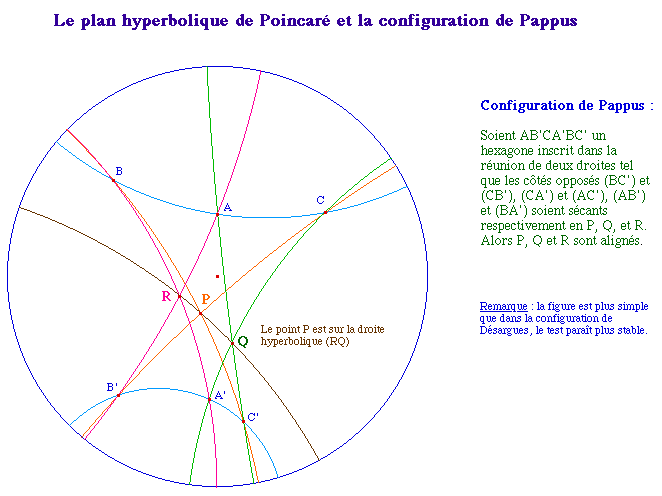
 PappusH.fig (PC) ou
PappusHM.fig (Mac)
PappusH.fig (PC) ou
PappusHM.fig (Mac)
Le plan hyperbolique et la configuration de
Fano
Quand un plan métrique est
plongé dans son plan idéal projectif, il vérifie
toujours la propriété de Fano : les trois points
diagonaux d'un quadrangle (4 points) ne sont pas
alignés.
Fano a montré que cette
propriété est équivalente au fait que le corps
construit soit de caractéristique différente de 2. On
en déduit alors que le point L construit comme ci-dessous ne
dépend que de A, B et I et est indépendant de C et
D.
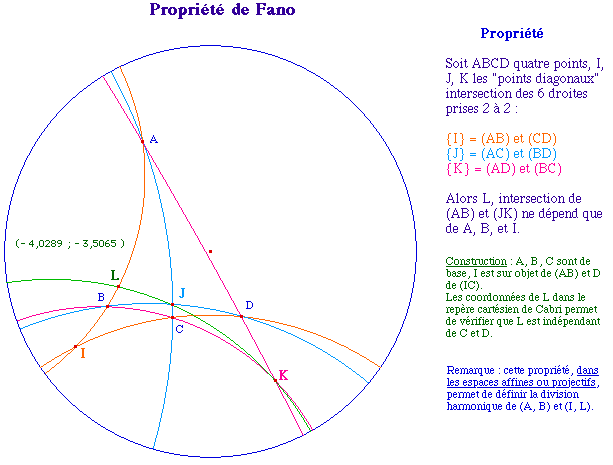
 FanoH.fig (PC) ou FanoHM.fig
(Mac)
FanoH.fig (PC) ou FanoHM.fig
(Mac)
[II.1. Droites et segments
hyperboliques] [II.3 -
Orthogonalité] [II.4 -
Premiers exemples d'utilisation]
[I. Introduction]
[III. Le cercle]
[IV. Les angles]
[V. Constructions]
[VI. Exercices]
[Retour aux GNE]
 Menu
général
Menu
général

![]() Desarg1.fig (PC) ou Desarg1M.fig
(Mac)
Desarg1.fig (PC) ou Desarg1M.fig
(Mac)

![]() Desarg2.fig (PC) ou Desarg2M.fig
(Mac)
Desarg2.fig (PC) ou Desarg2M.fig
(Mac)

![]() Desarg1.fig (PC) ou Desarg1M.fig
(Mac)
Desarg1.fig (PC) ou Desarg1M.fig
(Mac)

![]() Desarg2.fig (PC) ou Desarg2M.fig
(Mac)
Desarg2.fig (PC) ou Desarg2M.fig
(Mac)

![]() PappusH.fig (PC) ou
PappusHM.fig (Mac)
PappusH.fig (PC) ou
PappusHM.fig (Mac)

![]() FanoH.fig (PC) ou FanoHM.fig
(Mac)
FanoH.fig (PC) ou FanoHM.fig
(Mac)