Le livre I des éléments d'Euclide contient les axiomes, postulats de base de la géométrie "euclidienne", et les propositions relatives à la notion de parallélisme. Il comprend :

35 définitions, dont la dernière est :

Définition 35 : Les parallèles sont des droites qui, étant situées dans un même plan, et étant prolongées à l'infini de part et d'autre, ne se rencontrent ni d'un côté ni de l'autre.

 

6 postulats et 9 notions communes, dont le fameux cinquième :

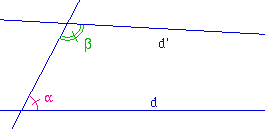
Postulat 5 : Si une droite, tombant sur deux droites, fait les angles intérieurs d'un même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits. Ce postulat est par la suite plus souvent énoncé sous la forme : "Par un point il passe une et une seule parallèle à une droite donnée".

 

48 propositions. Les 28 premières propositions et la 31^e n'utilisent pas le cinquième postulat. C'est en particulier le cas des trois "cas d'égalité des triangles" (Propositions 4, 8 et 26) qui seront donc vrais en géométrie hyperbolique, mais toutes les autres (29, 30, 32 jusqu'à 48) utilisent ce postulat. Voyons celles qui nous concernent directement ici :

Proposition 27 : Si une droite, tombant sur deux droites, fait des angles alternes égaux entr'eux, ces deux droites seront parallèles. Cette proposition permet de montrer que deux droites sont parallèles, sans avoir à utiliser la définition, c'est-à-dire, sans "les prolonger à l'infini". Elle est aussi vraie en géométrie hyperbolique.

Proposition 31 : Par un point donné, construire une ligne parallèle à une droite donnée.

Cette proposition 31 est un problème de construction qui établit l'existence de parallèles sur la base de la condition suffisante de la propriété 27 ci-dessus, et que par un point, il passe au moins une parallèle à une droite donnée.

 

Toutes les autres propositions utilisent le 5° postulat, soit directement, soit par l'intermédiaire d'une proposition obtenue avec son utilisation, à commencer par la réciproque de la proposition 27 :

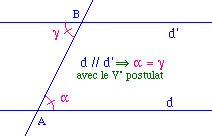Proposition 29 : Une droite qui tombe sur deux droites parallèles, fait les angles alternes égaux entr'eux, l'angle extérieur, égal à l'angle intérieur opposé et placé du même côté, et les angles intérieurs placés du même côté, égaux à deux droits. Cette proposition découle immédiatement du cinquième postulat dans une preuve par l'absurde, et c'est la première où il intervient.

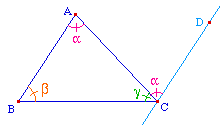
Proposition 30 : Les droites parallèles à une même droite sont parallèles entr'elles. Conséquence : Par un point extérieur à une droite, il passe au plus une parallèle à cette droite. Comme la proposition 31 est indépendant du 5° postulat, cette conséquence amène à l'autre écriture de ce postulat indiquée ci-dessus. Preuve de la conséquence et de son équivalence avec le V° postulat. Le parallélisme comme relation d'équivalence, et donc la notion de direction de droites, sont ainsi directement liés au V° postulat.

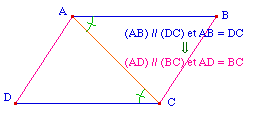
Proposition 32 : Les trois angles intérieurs d'un triangle sont égaux à deux droits.   Conséquence : La somme des angles d'un quadrilatère est 4 droits.

Proposition 33 : Les droites qui joignent, des mêmes côtés, des droites égales et parallèles, sont elles-même égales et parallèles. Proposition 34 : Les côtés et les angles opposés des parallélogrammes sont égaux entr'eux, et la diagonale les partage en deux parties égales.

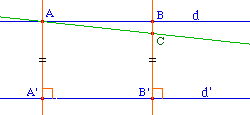Conséquence : Deux droites parallèles sont équidistantes. Cette propriété a plusieurs fois été prise comme définition des droites parallèles. Mais alors, l'existence même de droites parallèles nécessite une propriété équivalente au V° postulat.

En fait, ces propositions - ainsi que les conséquences mentionnées - sont chacune, équivalentes, au V° postulat, à la nuance près du cas ci-dessus.

Le fait que ces propositions - ou certaines d'entre elles - soient, par exemple, réciproques d'une proposition antérieure, indépendante dudit postulat, a à la fois sensibilisé les premiers commentateurs sur la question de la démontrabilité de ce postulat, et en même temps jeté une certaine confusion quant à la nécessité d'une preuve, puis quant à la production de cette preuve, et ceci même assez tardivement puisque dans les 13 éditions de sa "Géométrie", Legendre lui-même a parfois "montré" le postulat, et l'a parfois "admis".

La bibliothèque du vatican met en ligne quelques copies d'ouvrages grecs, dont le manuscrit "de Peyard" des éléments d'Euclide

Disponible à http://www.task.gda.pl/expo/vatican.exhibit/exhibit/d-mathematics/Greek_math.html (image JPEG de 605 Ko - texte et preuve de la proposition 47 : théorème de Pythagore)

 

Voir aussi la mise en ligne des 13 livres d'Euclide,
en géométrie dynamique (Applets Java) par David Joyce. 

Menu général