Quelques équivalences du V° postulat
(d'aprés une compilation de Jean Luc Chabert)
[Présentation chronologique] [Livre I d'Euclide] [Commentateurs] [Précurseurs][Fondateurs][Synthèses]
[Retour aux GNE] [Références utilisées] [Menu général]
 |
|
[Présentation chronologique] [Livre I d'Euclide] [Commentateurs] [Précurseurs][Fondateurs][Synthèses]
[Retour aux GNE] [Références utilisées] [Menu général]
 |
|
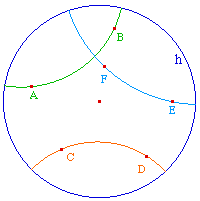
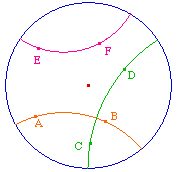
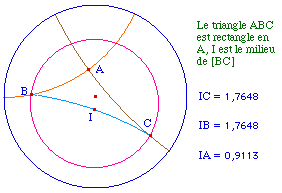
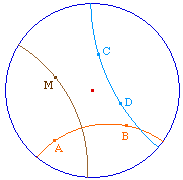
Les illustrations de droite sont des infirmations de ces propriétés en géométrie hyperbolique, dans le modèle du disque de Poincaré. Des liens permettent d'accéder directement aux approches constructives mentionnées.
|
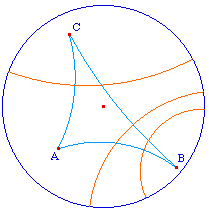 |
grande que l'on veut. |
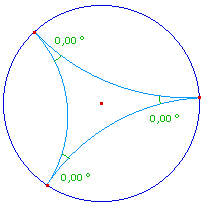 |
ayant un côté de longueur donnée et des angles égaux à ceux du triangle initial |
|
dans un demi-cercle est droit. |
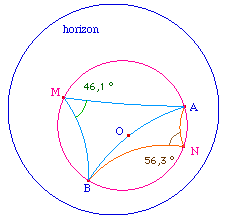 |
quadrilatère est égale à quatre droits. |
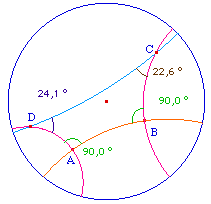 |
|
 |
![]()
être parallèles à une même droite. |
 |
|
 |
|
|
toujours une droite équidistante de la première. |
|
et situé d'un même côté de cette droite est une droite. |
|
|
|
une droite qui coupe les deux côtés de l'angle. |
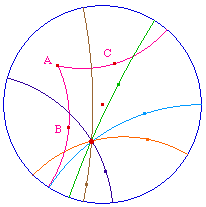 |
à une sécante commune se coupent. |
 |