Introduction aux
modèles hyperboliques plan
3 - Du modèle de
Klein-Beltrami au disque de Poincaré
3.a. Le principe sur les points et
droites - conséquences
3.a. Points et droites - Conséquences |
3.b. Exemple des cercles |
3.c. Une construction basée sur
ce passage
1. Présentation des modèles et
de leurs symétries orthogonales | 2. Les axiomatiques
possibles
[Construction dans le
modèle du disque de Poincaré] [Constructions
dans le modèle de Klein-Beltrami] [Version
Java]
[Historique sur
les GNE] [Retour aux
GNE] [Références
utilisées] [Menu
général]
Principe
général
|
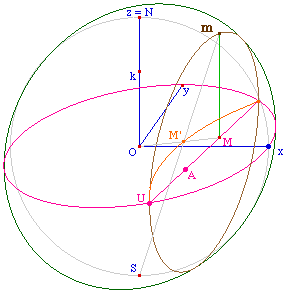
Sur un cercle horizon de Beltrami - l'équateur
(xOy) - on construit une sphère - ci-contre en
perspective cavalière.
À partir d'un point M du disque de Beltrami, on
construit sa projection m sur l'hémisphère
Nord, que l'on transforme à nouveau en M' sur le
disque équateur par projection centrale de centre le
pôle Sud.
Comme nous allons le vérifier dans la suite, le
lieu de M' est un cercle orthogonal à l'horizon.
 Modele03.fig
Modele03.fig
La suite de cette partie propose de détailler
cette première construction et de vérifier
expérimentalement que nous sommes bien dans le
modèle de Poincaré.
On peut aller directement à la
conclusion
|
Construction de la figure
précédente
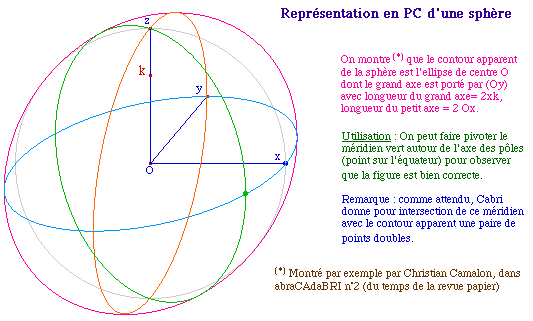
Contour apparent d'une
sphère en PC (méthode
proposée par Christian Camalon)
 Sphere.fig ou Sphere.mac
ou EquaCApp.mac (équateur
et contour apparent)
Sphere.fig ou Sphere.mac
ou EquaCApp.mac (équateur
et contour apparent)
|
Image d'un
point
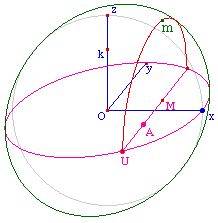
On se donne deux points U sur l'équateur et A
à l'intérieur du disque de Beltrami. et M un
point sur la droite (UA) du modèle.
Par une macro réalisée à partir de
la calculatrice, on construit m
sur l'hémisphère nord de la sphére. Le
lieu de m semble être une
ellipse - c'est bon signe - ce que l'on Cabri-confirme
rapidement en prenant 5 points autres que
m sur le lieu et en
vérifiant que m
appartient bien à l'ellipse.
 Modele01.fig ci-contre
ou Modele02.fig avec la
conique "lieu"
Modele01.fig ci-contre
ou Modele02.fig avec la
conique "lieu"
 PtSurS.mac d'objets
initiaux O, x, y, z, M, la droite (Ox)
PtSurS.mac d'objets
initiaux O, x, y, z, M, la droite (Ox)
|
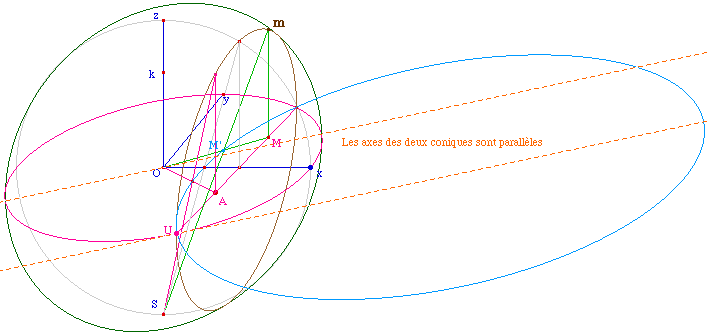
Puis on construit M' comme indiqué plus haut (Principe
général). On s'intéresse alors au lieu de M'. En
construisant trois autres points, avec les extrémités
du lieu on vérifie qu'une ellipse recouvre ce lieu. De plus,
on vérifie que le grand axe de cette ellipse et celui de
l'équateur sont parallèles : on a bien l'image d'un
cercle dans la perspective cavalière de rapport k et d'angle
xOy.
Le modèle de Poincaré en
perspective cavalière
 Modele04.fig
Modele04.fig
Passage en vraie grandeur
On place désormais l'équateur en vraie grandeur :
cercle de centre O' de rayon [Ox], et par une macro
 TransKvP.mac
(réalisée géométriquement, et contenue
dans la figure ci-dessous) on construit les images des
différents points U, A, M et V.
TransKvP.mac
(réalisée géométriquement, et contenue
dans la figure ci-dessous) on construit les images des
différents points U, A, M et V.
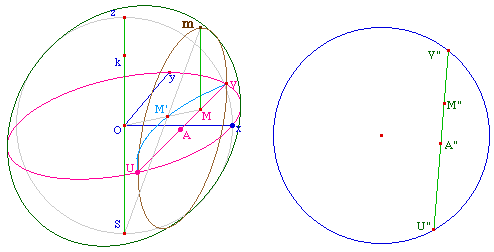
 Modele05.fig
Modele05.fig
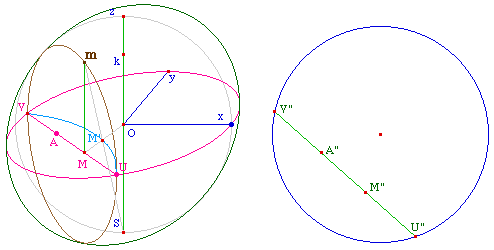
On applique alors la macro TransKvP.mac
au point M' : objets initiaux O, x, y, z, O', centre du modèle
de Poincaré, et un point du modèle de Klein. La macro
renvoie le point correspondant N dans le modèle de
Poincaré.
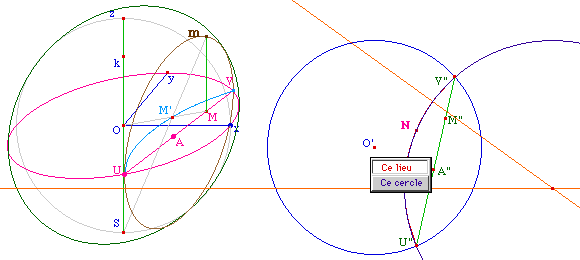
Expérimentalement, le lieu de N est bien un cercle, comme
entrevu plus haut, et qui plus est un cercle orthogonal à
l'horizon comme illustré ci-dessous.
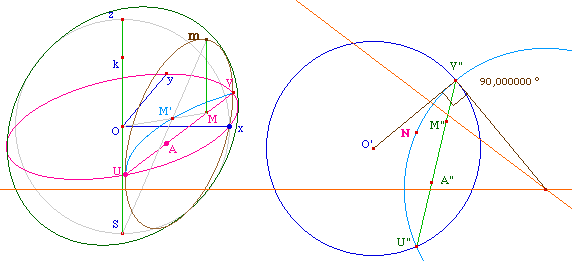
 Modele06.fig
Modele06.fig
Conclusion
En fait, la figure ci-dessus illustre un passage simple et rapide
d'un modèle à l'autre, sans avoir à utiliser de
sphère :
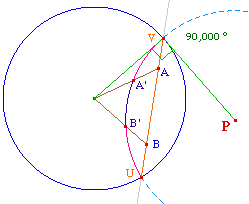
|
Soit [AB] un segment du modèle de
Klein-Beltrami (KB), comment construire, dans le même
cercle horizon, une correspondance [A'B'] du
modèle de Poincaré (P) ?
La réponse est trés simple, la droite (AB)
dans KB est aussi la droite idéale (UV). Soit P son
pôle par rapport au cercle. Alors - question de
cercles orthogonaux - le cercle de centre P passant par U
est orthogonal à l'horizon, il correspond à la
droite associée (UV) dans le modèle de
Poincaré.
D'aprés la figure ci-dessus (où, à
gauche, M' est sur le segment [OM]), les points A'
et B' sont les intersections avec cette P-droite des
segments euclidiens [OA] et [OB] où O
est le centre de l'horizon des deux modèles.
On passe bien entendu aussi aisément du
modèle de Poincaré à celui de
Klein-Beltrami puisque pour une droite donnée les
points U et V sont communs aux deux modèles ainsi que
P qui est à la fois le pôle de la droite par
rapport au cercle et le centre du cercle orthogonal passant
par ces deux points idéaux.
|
3.a. Points et droites - Conséquences | 3.b.
Exemple des cercles | 3.c.
Une construction basée sur ce passage
1. Présentation des modèles et
de leurs symétries orthogonales | 2. Les axiomatiques
possibles
[Construction dans le
modèle du disque de Poincaré] [Constructions
dans le modèle de Klein-Beltrami] [Version
Java]
[Historique sur
les GNE] [Retour aux
GNE] [Références
utilisées]
 Menu
général
Menu
général








