Introduction aux modèles hyperboliques plan

3 - Du modèle de Klein-Beltrami au disque de Poincaré

3.c. Exemple de la construction des tangentes communes par conjugaison

3.a. Points et droites - Conséquences | 3.b. Exemple des cercles | 3.c. Une construction basée sur ce passage

1. Présentation des modèles et de leurs symétries orthogonales | 2. Les axiomatiques possibles

[Construction dans le modèle du disque de Poincaré] [Constructions dans le modèle de Klein-Beltrami] [Version Java]

[Historique sur les GNE] [Retour aux GNE] [Références utilisées] [Menu général]

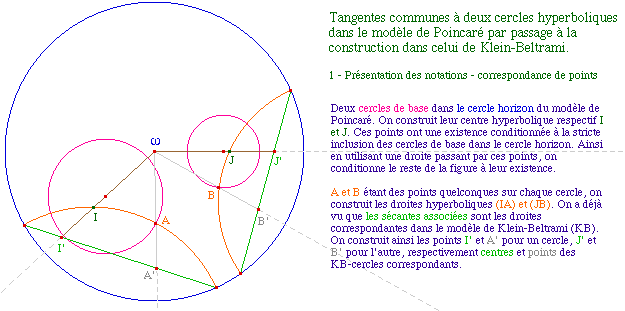
On se propose ici de construire les tangentes communes à deux cercles dans le modèle de Poincaré (P) à partir de leur construction dans le modèle de Klein-Beltrami (KB), par conjugaison : passage dans l'autre modèle, construction, passage réciproque.

Pour refaire cette figure, on a besoin des macros suivantes :

CtrHCrcl.mac (centre hyperbolique d'un cercle de base dans P), DrtHypG.mac (droite hyperbolique dans P, y compris par points idéalux),

CercleM2.mac (cercle dans KB), Tg2Conik.mac (tangentes communes à deux coniques)

Si on reprend les deux macros "tangentes communes extérieures" et "intérieures" laborieusement construites à cette page on peut noter que :
La construction directe peut se faire en 525 objets.
La construction faite ici prend 711 objets.
Dans cette construction, les tangentes communes sont 4 droites hyperboliques, alors que dans la construction proposée à la page ci-dessus, on a 8 droites qui existent exclusivement les unes des autres par groupe de 4. La construction de cette page est donc plus satisfaisante dynamiquement parlant.
Enfin la construction proposée ici par conjugaison est élémentaire alors que ce n'était pas le cas dans la construction directe.

TCConj.mac (pour Tangentes Communes par Conjugaison)

3.a. Points et droites - Conséquences | 3.b. Exemple des cercles | 3.c. Une construction basée sur ce passage

1. Présentation des modèles et de leurs symétries orthogonales | 2. Les axiomatiques possibles

[Construction dans le modèle du disque de Poincaré] [Constructions dans le modèle de Klein-Beltrami] [Version Java]

[Historique sur les GNE] [Retour aux GNE] [Références utilisées]

3 - Du modèle de Klein-Beltrami au disque de Poincaré

3.c. Exemple de la construction des tangentes communes par conjugaison

Passage de Poincaré vers Klein-Beltrami

Les deux KB-cercles et leurs tangentes communes

Retour à la construction dans le disque de Poincaré

Menu général