Modèle hyperbolique de Poincaré
IV. Les angles

IV.1.b - Bissectrices extérieures - cercles exinscrits

[IV.1.a - Bissectrices intérieures - Cercle inscrit]

[IV.2 - Mesure et consruction d'angles] [IV.3 - Rotations] [IV.4 - Polygones réguliers] [IV.5 - Pavages] 

[I. Introduction] [II. Les droites] [III. Cercles et distance] [V. Constructions] [VI. Exercices]

[Retour aux GNE] [Menu général]

 

Bissectrices extérieures - Cercles exinscrits hyperboliques

a - Construction des bissectrices extérieures. Faisceau de droites.

 

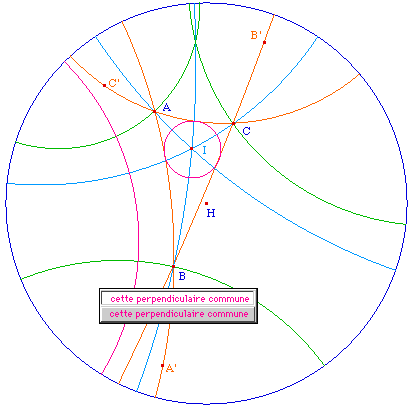
Pour construire les bissectrices extérieures, il ne faut pas prendre les perpendiculaires aux intérieures car leur orthogonalité, dans le cas euclidien, est une conséquence de la somme des angles d'un triangle. On peut - comme ci-contre - prendre les symétriques des sommets du triangle. Par exemple A' symétrique de A par rapport à B, et tracer la bissectrice intérieure de A'BC.

BiIntExt.mac : objets initiaux A, B, C, OAB, OBC, OAC et l'horizon. Objets finaux : les six bissectrices.

TRdBisIE.mac: objets initiaux : A, B, C, l'horizon. Objets finaux : les trois droites support du triangle, les six bissectrices.

Deux bissectrices extérieures et la bissectrice intérieure correspondante forment un faisceau : elles sont concourantes ou ont une perpendiculaire commune ou encore parallèles au sens de Bachmann, ie concourantes en un point idéal. Ce résultat a été montré plus généralement dans la présentation de l'axiomatique de Bachmann.

Remarquons que, si deux des trois droites concernées sont sécantes, par des arguments d'équidistance aux droites, la troisième passe par le point d'intersection.

HAngl05a.fig

b - Les cercles exinscrits

HAngl05b.fig (25 Ko)

c - Propriétés métriques

 

 

HAngl05c.fig (47 Ko - 1513 objets)

 

Point de vue géométrique pour aborder ces propriétés métriques

 

HAngl05d.fig (33 Ko - figure issue de "O5b")

 

Cette propriété sera abordée en exercice. Notons qu'il découle de ce résultat et du point de Gergonne hyperbolique que l'on a aussi le :

 

HAngl05e.fig (28 Ko, simplifiée par rapport à la précédente)

 

En plus de ceux-ci, d'autres résultats seront proposés en exercices.

 

[IV.1.a - Bissectrices intérieures - Cercle inscrit]

[IV.2 - Mesure et consruction d'angles] [IV.3 - Rotations] [IV.4 - Polygones réguliers] [IV.5 - Pavages] 

[I. Introduction] [II. Les droites] [III. Cercles et distance] [V. Constructions] [VI. Exercices]

[Retour aux GNE]

 

Menu général