Il s'agit, par des arguments un peu plus fins, de reprendre cette construction par axe radical, en amélioration l'utilisation "aux bornes", c'est-à-dire quand l'un des deux points P ou Q n'existe pas.

Etat de la construction actuelle

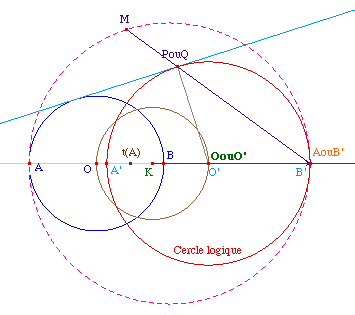
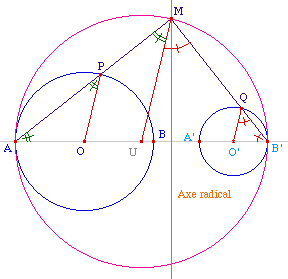
Le principe est de construire un point PouQ, intersection du segment [M AouB'] avec un cercle CouC'. Pour cela, nous allons simplement construire un point AouB' et le point OouO' et cela sera suffisant. La tangente commune étant alors la perpendiculaire en PouQ au segment [OouO' PouQ].   Allons-y ...   Si vous souhaitez faire la figure vous-même (ce qui ne demande que quelques instants) vous pouvez partir d'une figure épurée : Lancer la figure TgtEpur.fig nettoyée.

Construction du point AouB'

Considérons t(A) le translaté de A dans la translation de vecteur O'B'. Alors le cercle le plus grand est celui de centre O si t(A) est entre A et O, et c'est celui de centre O' sinon. Pour construire un unique point, qui soit sur A si le cercle passant par A est le plus grand ou sur B' dans l'autre cas, il suffit de construire l'intersection du cercle de diamètre [AB'] avec la demi-droite [O t(A)). Nous avons donc - déjà - notre point AouB'.

Construction du point OouO'

De la même manière soit K le milieu de O et O'. Alors la demi-droite [K AouB') coupe le cercle de diamètre [OO'] - de centre K - en le point OouO' cherché. Le cercle de plus grand rayon est donc le cercle de centre OouO' passant par le point AouB'. Et le segment [M AouB'] coupe ce cercle en le point PouQ cherché.

Construction des tangentes communes extérieures

Cette technique permet par exemple de classer 2, puis 3 cercles selon leurs rayons. Cela a été fait dans la page Comparaison de 3 cercles d'Alice. Cette dernière construction est utilisée à son tour pour transformer en méthode dynamique une construction statique de Viète sur la construction des cercles tangents à trois cercles.

Merci à Dominique Tournès d'avoir insité pour qu'abraCAdaBRI recherche une telle amélioration ... que de conséquences réalisées grâce à ce souhait ...

Menu général