L'objectif ici est de renvoyer sur 3 cercles, trois autres cercles qui sont spécifiquement pour le premier celui de plus petit rayon, pour le second celui de rayon intermédiaire et pour le troisième, celui de plus grand rayon.

La démarche est celle initiée dans la recherche des tangentes communes à deux cercles et plus particulièrement dans le traitement particulier pour que la construction existe quand les cercles sont tangents intérieurement. Nous proposons simplement ici une généralisation de cette page.

Le cas de deux cercles

  

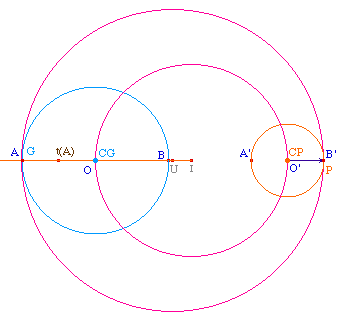
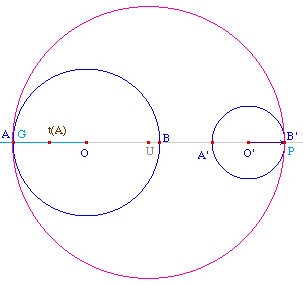
Etant donnés deux cercles de centres respectifs O et O', l'intersection d'un cercle avec la droite des centres oriente cette droite, et donc l'intersection de la droite avec le second cercle est aussi orienté de la même façon : sur l'illustration ci-dessous, les vecteurs AB et A'B' sont toujours orientés dans le même sens (soit R+-colinéaires). On considère alors le cercle de diamètre [AB'] de centre U. On se propose de renvoyer deux point G et P sur A ou B', G étant celui de ces deux points qui appartient au cercle le plus grand, P étant celui qui appartient au cercle le plus petit. Soit t(A) le translaté de A de vecteur O'B'. Le cercle de centre A est le plus grand si t(A) est entre O et A, c'est le plus petit sinon. Autrement dit le point G est l'intersection de la demi-droite [O t(A)) avec le cercle de diamètre [AB']. Bien-sûr, P est alors le symétrique de G par rapport à U. La figure Comp2Ca.fig pour vérifier ...

On peut alors faire la même chose pour les centres : soit I le milieu de O et O'. La demi-droite [IG) coupe le cercle de diamètre [OO'] en CG le centre du grand cercle qui est en O si G est en A et en O' si G est en B'. Si on note CP le symétrique de CG par rapport à I, le grand cercle est le cercle de centre CG passant par G - ce sera dans la suite le cercle en bleu clair - et le petit est le cercle de centre CP passant par P - qui sera dans la suite en orange.   La figure Comp2Cb.fig pour tests. On transforme cette figure en macro, en prenant soin de cacher les points G et P constitutifs, mais en rendant les centres dans la macro : La macro Compar2C.mac pour l'appliquer à trois cercles.

 

Cas de trois cercles

On commence par appliquer deux fois la macro précédente, en étant attentif à la seconde application : la première fois entre deux cercles quelconques, la seconde entre le plus grand des deux (bleu clair) et le troisième. Alors le bleu clair de la seconde application est le plus grand des trois. On peut le nommer ainsi. Mais il ne faudrait pas croire que cela puisse être suffisant car pour l'instant, le troisième cercle cliqué ne pourrait jamais être le plus petit puisqu'il n'est comparé qu'avec le plus grand des deux autres.   La figure Comp3Ca.fig partielle pour effectuer des tests.   On remarquera que le second cercle sous le cercle "moyen" dans l'illustration est bleu - par la couleur de son nom - car c'est le résultat de l'application de la seconde macro de comparaison qui modifie - dans la version actuelle de Cabri - la couleur des objets initiaux.

Pour finir la comparaison, il suffit de comparer le plus petit de la seconde application de la macro - le "ce cercle" orange sur l'illustration, avec le résultat de la première macro sur l'autre cercle. On décide alors de mettre en rose le cercle intermédiaire, et de conserver en orange le plus petit :   La figure Comp3Cb.fig finale, nettoyée des cercles et centres intérmédiaires.   La macro Compar3C.mac

Cette page a été réalisée pour illustrer que l'on peut réaliser une construction dynamiquement correcte de la méthode de Viète pour résoudre un problème d'Apollonius : la construction des cercles tangents à trois cercles donnés (en dehors d'une utilisation de l'inversion).

Menu général