1 -Nécessité de la Géométrie logique

 [2 - L'existence comme critère logique] [3 - Le Ping et le Pong] [4 - Un premier exemple]

En guise d'introduction, nous proposons dans cette page deux exemples de situations où l'intervention d'une démarche de géométrie logique est naturelle. Les figures d'illustration en téléchargement proposent, dans le même document, la situation avec et sans intervention de macros logiques.

Domaine de validité d'une construction

La situation est la suivante : soit un segment [AB] et I un point. On se propose de construire un point C tel que le triangle ABC ait I comme centre du cercle inscrit. (AI) et (BI) étant alors les bissectrices du triangle ABC, on construit A' et B' les symétriques de A et B par rapport à (BI) et (AI). Les droites (AA') et (BB') se coupent en un point C solution comme clairement illustré ci-contre. Un exercice traité de cette façon dans un environnement papier crayon est en général accepté, car le point I est - de fait - donné.

Avec Cabri, le point I étant quelconque dans le plan, on est amené à observer que les bissectrices que l'on a construites ne sont pas toujours les bissectrices intérieures du triangle cherché. Par exemple sur l'illustration ci-contre ce sont clairement les bissectrices extérieures, le point I devient centre d'un des cercles exinscrits au triangle ABC, et il n'y a pas de solution pour un éventuel cercle inscrit. Cela signifie que la construction précédente doit être conditionnée à son domaine de validité. La situation sera traitée plus loin (Premiers exemples : le cercle inscrit). Il s'agit ici seulement d'illustrer cette nécessité de la géométrie dynamique. AliceI1.fig qui permet de voir le problème et sa solution

Gestion des différents cas d'une situation

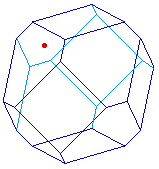
Alors qu'en réalité, quand le point qui définit la troncature passe d'une moitié de l'arête à l'autre, l'algorithme change. Dans l'état de la troncature ci-contre, il faut effectivement prendre en compte - par exemple - que les parallélogrammes obtenus par l'algorithme précédent deviennent des faces effectives. Autrement dit, sur une même figure, il faut pouvoir réaliser deux algorithmes différents selon la position d'un point mobile. Là encore l'illustration proposée en téléchargement sera étudiée en détail plus loin. Il s'agit ici d'illustrer seulement que le dynamisme des figures Cabri nécessiteun traitement spécifique des constructions. AliceI3.fig qui permet de voir cette question de la troncature et sa résolution dans Cabri.

  [2 - L'existence comme critère logique] [3 - Le Ping et le Pong] [4 - Un premier exemple]

Menu général