1 - Exemple d'introduction du cercle inscrit

  [Présentation de ce chapitre]
[2 - Troncature du cube] [3 - Section d'un tétraèdre] [4 - Segments dans l'espace]
[5 - Tiroirs d'une commode] [6 - Cube opaque en rotation]

Pour transformer la figure proposée en "figure logique", vous aurez besoin de la macro Intérieur Cercle que vous pouvez charger depuis votre disque dur, ou directement depuis abraCAdaBRI.

Charger la macro Intérieur Cercle

Rappel de la figure de départ

La situation est la suivante : soit un segment [AB] et I un point. On se propose de construire un point C tel que le triangle ABC ait I comme centre du cercle inscrit.

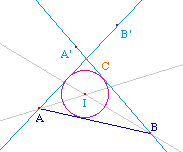
(AI) et (BI) étant alors les bissectrices du triangle ABC, on construit A' et B' les symétriques de A et B par rapport à (BI) et (AI). Les droites (AA') et (BB') se coupent en un point C solution comme clairement illustré ci-contre. Mais on a vu que c'est faux en général, le triangle construit peut être tel que ce cercle devient un cercle exinscrit au triangle. Pour construire la suite, il est nécessaire de Charger la figure Cabri en cours.

Manipulations sur la figure de départ

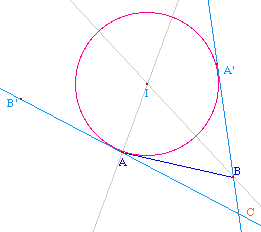On commencera donc à observer qu'en éloignant le point I du segment [AB], le triangle et le cercle construits ne correspondent plus à ce que l'on voulait construire : la figure précédente a un domaine de validité. On peut alors chercher à voir la frontière de ce domaine de validité : quand le point C n'existe pas, et se poser la question : quel est le lieu du point I pour lequel le point C n'existe pas ? C n'existe pas si les droites (AB') et (BA') sont parallèles, c'est-à-dire si (et seulement si) les angles géométriques B'AB et ABA' sont supplémentaires, c'est-à-dire si les angles moitiès IAB et ABI sont eux complémentaires, soit si et seulement si le triangle ABI est rectangle en I. Ainsi, il n'y a de solution que si I est intérieur au cercle de diamètre [AB].

Nous sommes prêts pour introduire une dose de géométrie logique qui permettra de respecter cette condition.

Introduction de points conditionnés

Deux méthodes ont possibles, soit refaire la figure, soit modifier celle déjà faite.

Pour refaire la figure, il faut construire séquentiellement :

le cercle de diamètre [AB]
le point Int sous I avec la macro Intérieur Cercle
reprendre la construction à la place de ce point Int au lieu du point I

Pour modifier la figure on peut opérer de la manière suivante :

construire le cercle de diamètre [AB]
prendre un autre point U de base à l'intérieur de ce cercle
construire le point Int sous U avec la macro Intérieur Cercle
redéfinir le point I comme identifié au point Int
rebaptiser le point U par I.

Nous vous invitons à réaliser la seconde construction, par modification de la figure initiale. C'est en effet une méthode générale :

À partir d'un second point (de base, ou sur objet), on réalise la contrainte d'existence conditionnelle qui correspond à la situation à traiter, puis on redéfinit le point de départ comme étant le point logique sous ce second point qui lui prend place.

On peut aussi préférer

Charger la figure ACInscr2.fig finale (mais ce serait dommage).

  [2 - Troncature du cube] [3 - Section d'un tétraèdre] [4 - Segments dans l'espace]
[5 - Tiroirs d'une commode] [6 - Cube opaque en rotation]

Menu général