1 - Test de parallélisme et applications

 [2 - Intégrité - OU de deux triangles]
[3 - Réunion de cercles et/ou triangles] [4 - OU exclusif et différence symétrique]

Le Chapitre des questions d'incidence d'Alice   On se propose ici d'explorer d'autres aspects de géométrie logique que ceux évoqués précédemment de distinction de cas ou de critère de validité d'une figure. Le thème qui soustend ces pages est une réalisation du OU de deux objets géométriques. Ces pages sont donc une transition entre les préoccupations précédentes et celles qui seront développées dans les macros booléennes. On y trouvera des constructions à la règle et au compas assez surprenantes, des questions nouvelles qui demanderaient à être un peu plus explorées qu'elles le sont ici. Dans une construction Cabri, il peut être nécessaire de vérifier que des conditions préalables d'application - ou plus simplement de sens - sont vérifiées. Certes, ces conditions sont souvent implicites. Par ailleurs "l'oracle" de Cabri peut aussi être utilisé. Les auteurs du logiciel ont choisi que les réponses de l'oracle ne peuvent être utilisées dans les constructions, par exemple comme objets initiaux de macros (ce qui est peut-être didactiquement sage). On se propose ici de réaliser des constructions conditionnées à de tels prérequis.

Par exemple, la construction des centres d'homothétie de deux segments, dans Cabri, n'est en général pas conditionnée à leur parallélisme considéré comme un implicite de la figure. Nous nous proposons dans cette page de faire entrer cet implicite - de parallélisme - dans la construction de la figure Cabri, et de voir quelques applications.

Un test de parallélisme

On se donne deux droites D₁ et D₂ et un point A sur objet de D₁. On se propose de rendre, sous A, un point D// qui n'existe que si les deux droites sont parallèles.

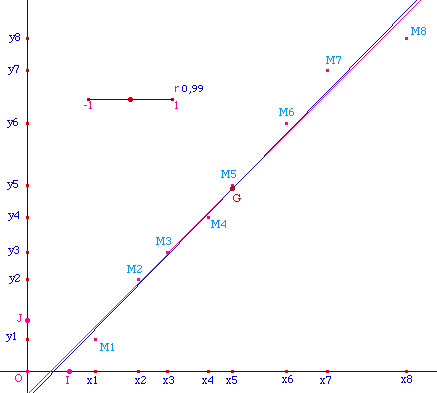
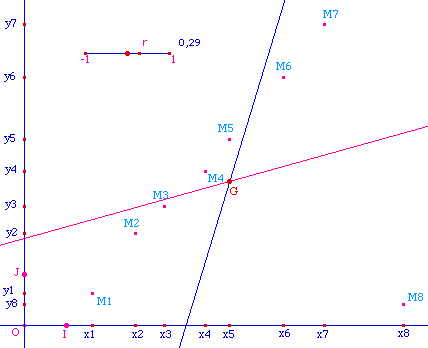
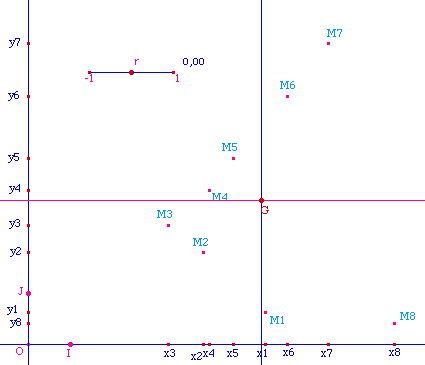
Lancer la figure Parall.fig pour tester son comportement. Charger la macro Parall.mac (Test de Parallèlisme)

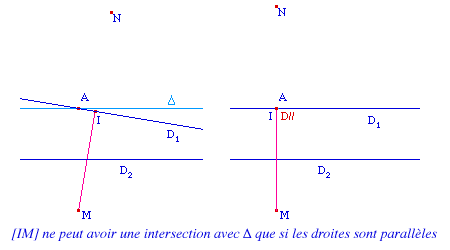
Soient M le symétrique de A par rapport à D2, N celui de M par rapport à D1, et I le milieu de M et N. I est un point de D1 tel que le triangle - s'il existe - MIA est rectangle en I, et donc MI > MA. Autrement dit tant que MIA en tant que triangle existe, c'est-à-dire tant que les deux droites D1 et D2 ne sont pas parallèles, le segment [MI] ne peut pas rencontrer la parallèle à D2 passant par A. L'intersection de cette droite et de ce segment n'est possible que si les droites D1 et D2 sont parallèles. Et cette intersection est alors un point sous A, puisque dans ce cas l'intersection est en I et que I est en A. Nous avons donc là une caractérisation du parallèlisme de deux droites sous la forme de la création d'un point, et ceci, en 5 objets intermédiaires seulement.

Remarque : la précision de Cabri est telle que cette macro n'est utilisable que quand les droites sont effectivement exactement parallèles : en pratique, sauf constructions explicites, dans le cas de droites de base, on l'utilisera pour des droites horizontales ou verticales : deux droites de base, en dehors de cas particuliers, ont peu de chance d'avoir exactement la même pente : on ne tombe pas à la souris, au pixel près, sur les doubles ou les triples de 127 et 61 pour une droite de pente proche de 2 par exemple.

Centre d'homothétie de deux segments

 

On se propose d'éviter de type de construction :   Pour cela, il suffit, sur une extrémité des segments de renvoyer un point conditionné au parallélisme des segments, et de construire les centres avec ce point conditionné, comme ci-contre. Lancer la figure CntrHSeg.fig pour la tester. Charger la macro CntrHSeg.mac pour l'appliquer.

Autre exemple d'application

Le test de parallèlisme peut aussi servir dans d'autres contextes, par exemple pour prendre en compte certains cas particuliers. Dans la situation ci-dessous, il s'agissait de montrer dynamiquement l'évolution des deux droites de régression linéaire, et du coefficient de corrélation, en fonction de la variation d'un seul critère, par exemple une abscisse ou une ordonnée de l'un des points du nuage (donc définis par les coordonnées).

La figure est un transfert dans Cabri II d'une figure de Cabri I (faite en 2.1 version Mac pour un cours en lycée) : tous les calculs algébriques pour arriver au coefficient de corrélation sont construits par des macros ... alors limitées à 50 objets. La figure se ferait bien plus facilement avec la calculatrice de Cabri II.

En déplaçant, comme ci-dessous, le seul point y8, on voit les droites s'écarter et le coefficient de corrélation diminuer.

Le problème s'est alors posé du cas du coefficient de corrélation nul, avec les droites orthogonales et surtout parallèles aux axes : comme elles étaient construites à partir de leur équation réduite, il est clair qu'une des deux droites disparaît, c'est d'autant plus dommage que c'est un cas intéressant à illustrer en classe. L'utilisation de la macro Test de parallélisme permet de se tirer d'affaire : si la première droite est parallèle à l'axe des abscisses, on construit l'autre droite à partir de l'existence du point de validation du parallélisme.

Lancer la figure CoefCorr.fig sur les coefficients de corrélation.

Remarque : Cette figure, assez longue à faire dans l'ancienne version de Cabri peut se faire plus facilement en Cabri II. On notera que l'on peut aussi faire apparaître le signe du coefficient de corrélation par un test d'appartenance à un segment.

 [2 - Intégrité - OU de deux triangles]
[3 - Réunion de cercles et/ou triangles] [4 - OU exclusif et différence symétrique]

Menu général