Les questions d'incidence d'Alice

2 - L'intégrilté d'Alice

 

 [1 - Test de parallèlisme - Applications]
[3 - Réunion de cercles et/ou triangles] [4 - OU exclusif et différence symétrique]

[Introduction à la géométrie logique] [Les macros logiques] [Premiers exemples significatifs]
[La Galerie d'Alice] [Constructions spécifiques] [Retour Alice] [Menu général]

 


 Cette fiche technique ouvre vers d'autres aspects de la géométrie logique. Une question avait longtemps "hanté" les soirées de feu abraCAdaBRI-papier sur la possibilité de créer des OU d'objets géométriques à la règle et au compas. Une solution générale, et particulièrement élégante, mais basée sur l'orientation dans Cabri II - donc fortement fonction des choix de transposition informatique de l'implémentation de l'orientation - est proposée dans la section sur les macros booléennes.

On se propose ici d'explorer ce terrain par des arguments euclidiens simples, sans orientation. Le premier OU à réaliser est celui de l'intégrité : un produit ab est nul si l'un des deux l'est. On commencera par ce point.


Vision géométrique de l'intégrité

 


La difficulté rencontrée, par rapport à un produit algébrique classique,vient de ce que la construction doit être opérante, même si les deux termes sont nuls. Pour cela il semble bien - mais abraCAdaBRI est prêt à modifier son appréciation dès qu'on lui montre le contraire - qu'une construction véritablement intrinsèque soit difficile à réaliser. Nous proposons une version non intrinsèque, suffisante pour les applications que l'on en fera.

O et I sont donnés et A est un point de la droite (OI). On note a = OA et b = OB. On veut construire sous O un point qui n'existe que si a est nul ou b est nul. C'est donc un premier OU de deux situations (et non pas encore de deux objets). Pour cela on réalise une possibilité de rendre compte que le produit ab est nul.

La parallèle à [IB] passant par A coupe la perpendiculaire à (IO) passant par O en K. Alors a ou b est nul, c'est-à-dire A ou B est en O si et seulement si K est en O. Or K est en O si et seulement si le cercle de centre I passant par K coupe le segment [IO] (argument proche de la démarche vue pour le test de parallélisme).

Les trois contextes "dessins" dans lesquels le point ab=0 doit exister sont les suivants. La construction a bien-sûr été faite pour être opérante aussi dans le troisième cas :

On considèrera que cette version n'est pas intrinsèque car en plus des points O, A et B, elle utilise une direction de référence (OI) sur laquelle on place l'un des deux nombres (a ici). En pratique cela suffit.


Lancer la figure Integre1.fig sur l'intégrité pour tester son comportement.

Charger la macro Integre.mac d'objets initiaux O, I, A et B, pour l'utiliser sur la figure suivante.

Remarque : dans ce type de situation de OU, si on a à faire vérifier (par exemple en formation) qu'un point X qui est bien toujours le même, y compris dans des situations de réapparition un peu "extrêmes", un bon moyen est de proposer la création d'un segment d'origine un point de base quelconque et d'extrémité ce point X : si le segment après avoir disparu réapparaît dans un autre contexte avec le point X, c'est bien qu'il s'agit du même point X dans ces deux contextes dessins différents. Cette remarque peut servir ci-dessus, et à la construction suivante.

 

OU de deux triangles

 

Soient deux triangles ABC, et A'B'C' et un point M. On se propose de construire ce que l'on appellera le OU de (l'intérieur de) deux triangles : un point sous M qui existe quand Mest dans l'un ou l'autre des deux triangles.

Pour cela, on utilisera une construction déjà faite dans les macros de base d'Alice, à propos de l'extérieur d'un triangle. La macro est différente de l'extérieur d'un triangle en ce sens que la partie finale de la construction ne nous intéresse pas.

Si vous voulez faire la figure en direct (très rapide, il s'agit d'appliquer seulement des macros antérieures) vous aurez besoin de

Charger la macro ExtTrOU.mac (Ext. Triangle pour OU) d'objets initiaux un triangle et un point M.

La macro précédente construit un point Z qui est confondu avec M si M est à l'intérieur du triangle et qui est différent de M s'il est à l'extérieur.

Rappel : on en déduisait une macro extérieur triangle en prenant justement la médiatrice de Z et de M, puis le symétrique de Z par rapport à cette droite.

Même si ce n'est pas utile pour la suite on peut revoir la construction (faire alors Back pour revenir).

 

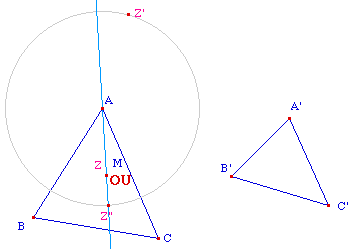
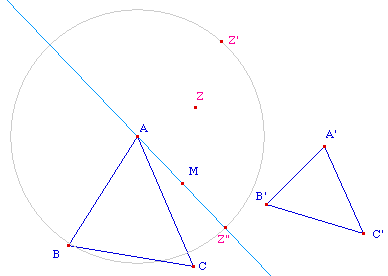
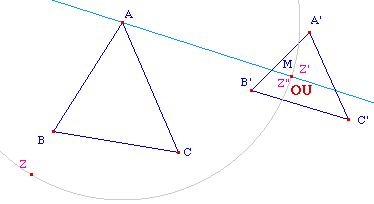
Dans l'illustration ci-contre, on a appliqué la macro Ext. Triangle pour OU au triangle ABC et au point M, elle a construit le point Z, puis on l'a appliquée à nouveau au triangle A'B'C' et au point M, ce qui a donné le point Z'. Pour appliquer la macro Intégrité à M, Z et Z', il faut une droite de référence, on prend la droite (AM). Il faut alors construire l'un des deux points sur cette droite. Comme par construction Z et M sont sur un même cercle, on choisit plutôt de placer Z' sur cette droite, par un cercle, ce qui donne le point Z".

On peut alors appliquer Intégrité à M, A, Z et Z", même dans le cas où le produit n'est pas nul, c'est-à-dire ici si M est à l'extérieur des deux triangles (comme l'illustration ci-dessus).

Quand M est à l'intérieur d'un des deux triangles le point construit (le point ab=0 de la macro Intégrité) est un point qui existe quand M est à l'intérieur des deux triangles.

On peut utiliser la remarque indiquée au pargraphe sur l'intégrité pour illustrer que le OU construit est bien le même point dans le triangle ABC et dans le triangle A'B'C'.

La figure OU2TR.fig

La macro OU2TR.mac (OU de deux triangles) pour l'appliquer à la figure suivante.

 

 

Quand Cabri sonde l'intérieur d'une étoile

 

Une étoile régulière à 6 branche se construit facilement à partir de deux triangles équilatéraux. On en déduit donc une construction de l'intérieur d'une étoile régulière à 6 branches ...

Lancer la figure IntEtoil.fig d'intérieur d'une étoile.

On peut observer l'apparition periodique du point intérieur quand les branches tournent autour du centre de l'étoile.

Certe, on s'éloigne largement d'applications en classe ici, voire même tout simplement mathématique. Néanmoins, il est intéressant de voir que l'on peut construire une figure à la règle et au compas qui donne un test d'intérieur d'une étoile régulière ...

 

 [1 - Test de parallèlisme - Applications]
[3 - Réunion de cercles et/ou triangles] [4 - OU exclusif et différence symétrique]

[Introduction à la géométrie logique] [Les macros logiques] [Premiers exemples significatifs]
[La Galerie d'Alice] [Constructions spécifiques] [Retour Alice]

 

Menu général