|
|
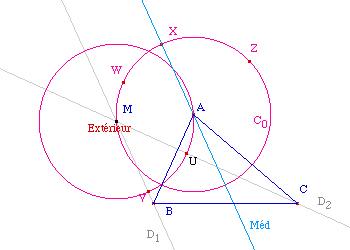
Le cercle de centre M passant par
A coupe la droite (MC) en U et la droite (MB) en V. L'angle
UMV est aussi l'angle géométrique BMC. Mais
pour reporter des angles géométriques, il faut
reporter des distances, c'est-à-dire utiliser des
cercles, de nouveaux cercles, sinon l'angle sera
orienté. Pour cela, on utilisera
systématiquement l'item Compas pour construire de
nouveaux cercles. On travaillera sur le cercle
C0, de centre A passant par M, et on reportera,
à partir de M, les différents angles
géométriques, ici dans le sens contraire au
sens trigonométrique.
Ainsi, Par Compas, le cercle de
centre M et de rayon [UA] - report de AMC - coupe
C0 en W. Le cercle de centre W et de rayon
[UV] - report de CMB - coupe C0 en X.
Enfin, le cercle de centre X et de rayon [AV] -
report de AMB - coupe C0 en Z (l'autre
intersection est nécessairement sur M).
Le point Ext est simplement le
symétrique de Z par rapport à la
médiatrice de [MZ]. On vérifiera que
ce point existe effectivement toujours à
l'extérieur du triangle, en passant dans les six
régions délimitées par les trois
droites supports du triangle, et qu'il n'existe pas à
l'intérieur.
|