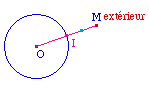2 - Extérieur d'un objet

 [1 -Intérieur d'un objet] [3 - Position dans le plan ou sur la droite] [4 - Premiers exos de macros]

Si vous souhaitez faire les figures en direct, vous aurez besoin de

Charger la macro Ping-Pong qui servira plusieurs fois.

Extérieur d'un cercle

 

Un point M est extérieur à un cercle de centre O ssi le segment [MO] coupe le cercle. Soit I ce point. La macro Ping-Pong appliquée sur I et M permet de construire sous M un point Extérieur cercle Lancer la figure ExtCerc.fig ou charger la macro ExtCerc.mac (utile pour la suite)

Extérieur d'un segment

 

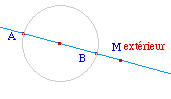Un point M d'une droite (AB) est extérieur au segment [AB] s'il est extérieur au cercle de diamêtre [AB]. On utilise donc la macro précédente Extérieur Cercle. On notera que si la macro est en réalité un Extérieur ]AB[, mais c'est suffisant à l'utilisation sauf peut-être si [AB] est horizontal ou vertical. Dans ce cas on peut avoir besoin d'affiner. Lancer la figure ExtSeg.fig ou charger la macro ExtSeg.mac

Extérieur d'un triangle

Dans la page précédente sur les intérieurs, Alice propose une macro logique testant l'intérieur d'un triangle. Sur la base de cette construction, après de multiples essais, on remarque que l'extérieur d'un triangle semble être irrémédiablement un OU de plusieurs situations disjointes, et on a du mal à imaginer une construction avec Cabri rendant compte de cette manière qu'un point est à l'extérieur d'un triangle.

Mais alors pourquoi essayer de construire une macro logique Extérieur Triangle si cela ne paraît pas aussi immédiat que le teste. L'idée vient, justement que, puisque l'on n'arrive pas à réaliser l'extérieur par un OU, on pourrait peut-être obtenir quelques résultats sur les OU en réalisant l'extérieur d'un triangle autrement, de manière plus intrinsèque, sans distinction de cas.

La question est donc : étant donnés un triangle ABC et un point M, y-a-t-il une caractérisation totalement symétrique en A, B et C, du fait que M est à l'extérieur du triangle ? La réponse est oui, et de manière élémentaire :

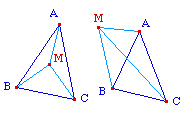Un point M est à l'intérieur du triangle ABC ssi la somme des angles géométrique AMB, BMC et CMA est égale à 2*pi;. Le point est à l'extérieur ssi cette somme est strictement inférieure à 2*pi;. Reste à traduire cette propriété en terme de test logique. On construit cette somme sur un cercle. M sera à l'extérieur ssi le point d'arrivée Z est différent du point de départ M. Et on a notre test : M est à l'extérieur ssi M et Z sont dictincts , soit ssi la médiatrice de [MZ] existe, ce qui permet de renvoyer un point sur M par un symétrique. Voir le détail de la construction esquissée ci-dessus.

Lancer la figure ExtTrian.fig finale ou charger la macro ExtTrian.mac

Cette macro est effectivement un exercice de style, mais elle nous permettra, dans l'item "Applications topologiques" d'Alice de réaliser le OU de l'intérieur de deux triangles.

Extérieur d'une conique

On sait qu'un point M est extérieur à une conique si sa polaire associée coupe la conique. La construction de l'extérieur est donc immédiat à partir de la polaire

Charger la macro Polaire d'un point

 [1 -Intérieur d'un objet] [3 - Position dans le plan ou sur la droite] [4 - Premiers exos de macros]

Menu général