 |
Soit Int le point sous le point M
qui rend compte que M est entre A et B au sens large obtenu
par la macro Interieur Segment. On peut avoir besoin d'un
point qui n'existe pas à l'une des
extrémités du segment, disons B.
|
 |
On pourrait faire la même chose en A à partir de la figure précédente. Toutefois, il y a un procédé bien plus simple pour l'appartenance à un segment ouvert.On vous propose ici de chercher, toujours à partir d'un point M sur objet d'une droite (AB), à construire sous M un point Int qui n'existe que sur l'intérieur ]AB[, et ceci en un seul objet intermédiaire.Il suffit donc d'explorer les menus de Cabri ...
|
 |
Etant donnés deux point A et B on cherche à construire un point sur l'un des deux qui n'existe que quand ces points sont confondus. Pour cela, on utilisera un troisième point O dont on sait qu'il n'est jamais confondu - pour l'application de la macro qui en résulte - avec l'un de ces deux points.On dispose donc de trois points de base O, A et B. Et on veut renvoyer un point A=B qui n'existe que si A et B sont confondus.
|
![]()


![]()
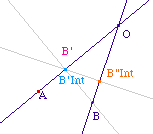 |
Soit B' la projection de B sur
(AO) et B'Int le point sous B qui n'existe que si B' est
entre A et O. B'Int n'existe que si B est dans une bande
délimitée par les perpendiculaires (comprises)
à (AO) passant par A et O.
|
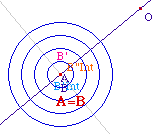 |
Pour rendre compte de l'égalité, qui ne se voit pas facilement à cause du curseur main de Cabri, sur cette figure on a élargi le champ visuel en construisant une "cible" de cercles concentriques quand il y a égalité des deux points A et B.
|