3 - Réunions de cercles et / ou triangles

  [1 - Test de parallèlisme - Applications]
[2 - Intégrité - OU de deux triangles] [4 - OU exclusif et différence symétrique]

Cette page poursuit ce qui a été fait dans celle sur l'intégrité. Nous avions vu la réunion (ou dira le OU) de l'intérieur deux triangles. Nous allons voir ici celle de (l'intérieur) deux cercles ou d'un cercle et d'un triangle.

Les figures proposées ici sont élémentaires à faire, il s'agit simplement d'appliquer quelques macros déjà faites. Si elle n'est pas déjà sur le disque dur, on aura en particulier besoin de

Charger la macro Integre.mac qui servira plusieurs fois.

Préliminaires sur le Minimum de deux points.

Pour obtenir le OU de deux triangles, nous avions utilisé l'existence d'un point Z construit à partir d'un point M tel que M et Z sont distants quand M est à l'extérieur du triangle et superposés quand il est à l'intérieur. Si on arrive à construire un point Z qui a les mêmes propriétés pour le cercle, l'application des macros donnera le résultat cherché.

Une idée (pas nécessairement la plus simple) consiste à renvoyer un point sur M quand M est à l'intérieur et l'intersection du cercle et de la demi-droite [OM) quand M est à l'extérieur (O étant le centre du cercle). Réaliser cela serait trés simple si on savait prendre le minimum de deux abscisses sur une droite. Or ceci est facile à faire : Soit (D) une droite d'origine O - on utilise ici l'orientation par défaut des droites de base de Cabri - et deux points A et B sur objet de cette droite. On veut construire un point Min qui se place sous celui des deux points A ou B qui a l'abscisse minimale (pour cette orientation par défaut). La figure Min2pts.fig. La macro Min2pts.mac d'objets initiaux une droite, son origine O, puis les points A et B.

On est prêt pour faire une réunion géométrique de deux disques très simplement

OU de deux cercles

 

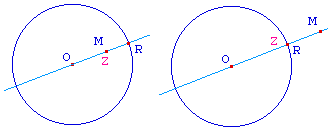Etant donné un cercle de centre O et M un point, on note R l'intersection de la droite (OM) et du cercle qui apparient en fait à la demi-droite [OM). En appliquant la macro Min de 2 points à la droite, O, M et R, on construit le point Z cherché en préambule.

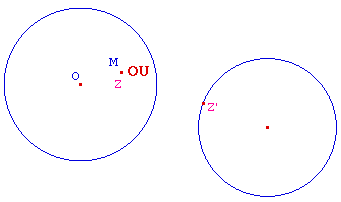Si on applique cette même macro à un autre cercle, et le même point M, on construit un second point Z'. On peut alors appliquer la macro Intégrité aux points M, O, Z (qui appartient par construction à la droite (OM), il n'y a donc pas de problème) et Z', on construit ainsi sous M un point OU qui n'existe que si M est à l'intérieur des deux cercles.   Lancer la figure OU2cercl.fig du OU de deux cercles (réunion de deux disques). Charger la macro OU2Cercl.mac ... mais ce serait dommage de ne pas réaliser ces dernières constructions soi-même.

OU d'un cercle et d'un triangle

  [1 - Test de parallèlisme - Applications]
[2 - Intégrité - OU de deux triangles] [4 - OU exclusif et différence symétrique]

Menu général