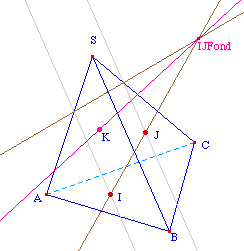
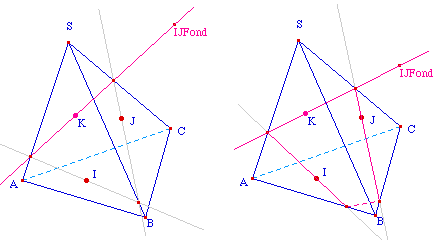
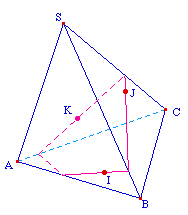
 |
Il s'agit de la construction d'une section d'un tétraèdre - base ABC, sommet S - par le plan passant par 3 points I, J, K des faces latérales, respectivement SAB, SBC et SCA. La construction a été effectuée avec les points I, J, K de base.Plusieurs méthodes sont
possibles, celle présentée ici repose sur le
principe de projection de la section sur l'une des faces
à couper.
|
 |
On projette deux points de la section selon l'arête commune aux face contenant ces deux points : ici on projette donc I et J sur le plan (SCA) selon l'arête (SB). La droite passant par les deux points obtenus est donc la projection de la droite (IJ) sur le plan (SCA) selon la direction (SB). Cette droite coupe la droite (IJ) en un point IJFond qui est l'intersection de la droite (IJ) avec le plan (SCA).Comme ce point IJFond appartient
au plan (IJK), la droite passant par lui et K aussi. Donc la
droite (IJFond K) est la trace de la section dans le plan
(SCA). Cette droite peut couper la face SCA de trois
façons différentes, puisqu'elle elle coupe 2
arêtes parmi trois.
|
|
|
On traite seccessivement chacun de ces trois cas, ce qui est trés rapide.Remarquons toutefois qu'un cas peut avoir deux sous cas, selon les intersections des droites en jeu sur les arêtes, comme l'illustration ci-dessous. En pratique, sur un tétraèdre, une section ne peut être qu'un triangle ou un quatrilatère. |
Menu général