 |
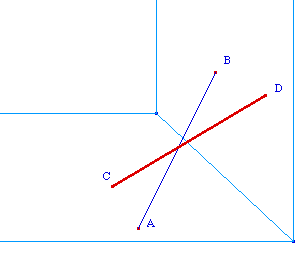
On dispose de deux segments [AB] et [CD] qui modélisent deux baguettes, dont les extrémités A et C sont sur un premier plan, horizontal, et les deux autres B et D sur un second plan, vertical. Dans le dessin en perspective cavalière, les deux segments se croisent. La question dans l'environnement papier/crayon était : lequel est au dessus de l'autre.Dans l'environnement Cabri on peut proposer la construction : dessiner en rouge le segment au dessus et en bleu celui en dessous. |
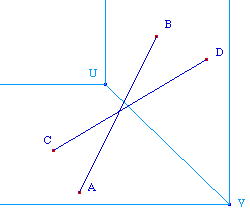 |
On se donnera quelques libertés d'action : les segments Cabri ne seront pas de taille fixe - autrement dit les points A, B, C et D seront des points de base - comme si, en classe, on illustrait notre construction avec des segments en ficelle en gardant dans la main 30 cm de plus pour changer les données de la situation : à sa façon, la manipulation directe a toujours existé en classe avant le passage sur informatique, heureusement ! Mais certainement pas dans l'environnement papier crayon ...
|
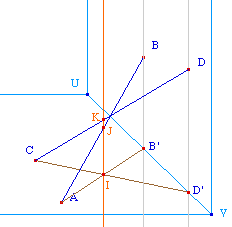 |
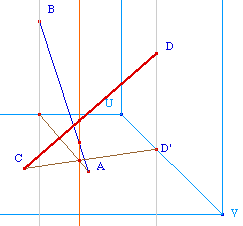
On construit les projections orthogonales des segments sur le sol (l'ombre des bâtons à midi). On les suppose sécantes en I. Ce point I étant sur l'intersection des projections orthogonales provient de deux points : J sur [AB] et K sur [CD].Il est clair que le segment le plus haut est celui qui contient le point, J ou K, le plus éloigné de I. Sur le dessin ci-contre, [CD] est au dessus de [AB].D'où l'idée d'une fin de construction conditionnée par la position des points I, J et K. |
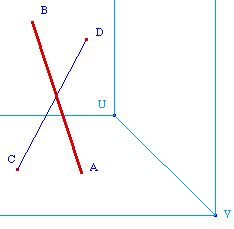 |
On peut ainsi envisager de transformer toute la figure en une macro pour l'appliquer à B et D sur le mur du fond :On transforme la figure précédente (dite "terminée") en macro, d'objets initiaux, les 4 points A, B, C et D, le segment [UV] et le segment vertical qui a été utilié pour les projections orthogonales. Comme objets finaux les segments rouges, tous les segments rouges : la version II de Cabri permet, dans les objets finaux, de modifier la figure en appuyant sur la touche de contrainte (touche Majuscule).En appliquant cette macros aux points quand B et D sont sur le mur du fond, on arrive à la figure ci-contre.
|
 |
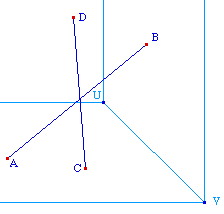
On a bien traité d'un coup le cas des deux segments sur le mur du fond, mais pour les y mettre, on déplace les point B et D séquentiellement. On a donc aussi à traiter le cas où l'un de ces deux points est sur un mur et l'autre sur l'autre mur.On est ramené à faire une nouvelle construction, en prenant soin de traiter dans ce cas de B sur le mur du fond et D sur le mur de droite, les deux sous cas [AB] est au dessus et [CD] est au dessus.On peut aussi préférer :
|
 |
|