2 - Troncature du cube

  [Présentation de ce chapitre]
[1 - Introduction du cercle inscrit] [3 - Section d'un tétraèdre] [4 - Segments dans l'espace]
[5 - Tiroirs d'une commode] [6 - Cube opaque en rotation]

Pour réaliser la figure proposée comme "figure logique", vous aurez besoin des macros Intérieur Segment et Ping-Pong que vous pouvez charger depuis votre disque dur, ou directement depuis abraCAdaBRI.

Charger les macros Intérieur Segment, Ping-Pong

Rappel de la situation à traiter

 

Il s'agit d'effectuer la troncature du cube par les sommets. On a déjà dit qu'il y a deux algorithmes selon que l'on est sur une moitié de l'arête qui contient le point définissant la troncature, ou sur l'autre moitié de cette arête. On voit ici que l'algorithme de base, à gauche, convient pour une moitié d'arête, et que pour l'autre moitié, il suffit de conserver les parallèlogrammes qui apparaissent à droite sur les six faces et simplement joindre les sommets des faces adjacentes.

La figure de départ

 

Que la construction soit faite avec un cube fixe ou avec un cube en rotation n'apporte strictement aucune différence. Aussi proposons nous de faire cette construction sur la base d'un cube en rotation. On travaillera donc sur la figure standard de la rubrique Espace pour ce qui est de la rotation du cube :   Qu'il convient de charger si vous ne l'aviez pas sur votre disque (RotCub.fig). Les figures seront représentées avec une face dans le plan frontal pour une meilleure lisibilité. On n'oubliera pas que le cube tourne avec le point Rot.

La troncature par les sommets

 

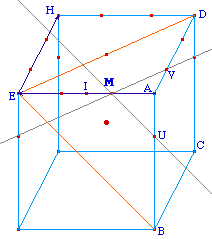Il s'agit de couper le cube à chaque sommet par un plan orthogonal à la grande diagonale du cube passant par ce sommet. La troncature donne donc, à cuaque sommet, des triangles équilatéraux. S'ils sont trop grands, ils se chevauchent, et c'est ce que l'on propose de prendre en compte ici. Dans toute la suite M est un point de base du segment [EA], I le milieu de ce segment. Les lignes de coupe, quelque soit la position du cube, est donné par la parallèle à [ED] passant par M pour la face de dessus, puis une autre parallèle, ici à [EB]. On obtient ainsi 3 points M, U, V qui représente la section du cube au sommet A. Pour les autres sommets - du haut - il suffit de prendre le symétrique de M par rapport à I et de faire des translations en utilisant seulement les vecteurs AE et EH. On ne reliera pas les segments à construire sont conditionnés à une position précise de M, mais ces points serviront aux deux branches de la figure.

Première branche de la troncature (cube adouci)

 

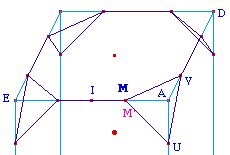On place M entre I et A, et on applique la macro Intérieur Segment à I, A, M afin de construire M' sous M qui rend compte que M est bien entre I et A. À partir de ce point M', on construit sous tous les points du haut - y compris ceux des arêtes verticlaes, un point conditionné à celle de M'. Et c'est à partir de ces points que l'on construit les segments.

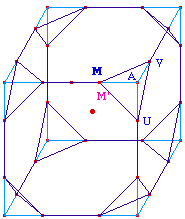Il suffit ensuite de faire le symétrique des 16 segments du haut par rapport au centre du cube et de rajouter les 4 segments sur les arêtes verticales pour avoir terminé cette permière branche logique de la troncature du cube. On peut aussi choisir de prendre la figure en cours de route et Charger la figure TrCbSom3.fig en l'état.

Seconde branche de la troncature (octaèdre adouci)

 

En plaçant M sur le segment [EI], on construit, encore avec la macro Intérieur Segment un point M" sous M qui rend compte que M est bien entre E et I. À partir de ce point M", on construit le segment [M"V] et son symétrique par rapport au centre de la face du haut : ce segment est aussi conditionné par l'existence de M". De même, en plaçant sous quelques autres points construits à partir de M des points conditionés par l'existence de M", et en utilisant les symétriques des segments, on arrive à la situation ci-contre en trés peu d'objets supplémentaires : on dispose des carrés d'intersection sur les trois faces visibles.

Les deux branches sont terminées, on dispose d'une figure de troncature qui contient les deux algorithmes de construction, sur la base d'une distinction de cas par la macro Intérieur Segment, et d'un conditionnement à ces cas par l'usage d'une existence conditionnelle que permet la macro Ping-Pong. La troncature par les sommet part du cube, arrive à l'octaèdre et passant par le cuboctaèdre, quand M est en I.   La figure TrCbSom6.fig finale.

On notera que cette troncature passe aussi par deux autres polyèdres semi-reguliers : le cube tronqué, et l'octaèdre tronqué. Ces deux polyèdres particuliers sont obtenus ici quand la position de M est telle que toutes les arêtes de la troncature sont de même dimension. Cette condition est facile à réaliser et peut faire l'objet d'une recherche en module au lycée : on construit alors le point N correspondant, et on redéfinit M comme étant ce point. Pour ce qui est de l'utilisation des macros logiques, on notera que l'on trouvera, dans la Galerie d'Alice, le traitement des parties cachées de cette troncature par les sommets.

 [1 - Introduction du cercle inscrit] [3 - Section d'un tétraèdre] [4 - Segments dans l'espace]
[5 - Tiroirs d'une commode] [6 - Cube opaque en rotation]

Menu général