3 -Le Ping et le Pong

 [1 - Nécessité de la Géométrie logique] [2 - L'existence comme critère logique] [4 - Un premier exemple]

Nous avons vu dans la page précédente, les principes de base pour réaliser des constructions logiques. En fait, l'arborescence des figures Cabri nous permet d'emboîter autant de "if then" qu'on le souhaite, avec l'existence d'un objet comme critère de test.

On peut construire ainsi des branches entières de figures Cabri qui ne dépendent chacune que de l'existence d'un point.

On se propose ici d'observer que l'on peut toujours facilement conditionner l'existence d'un point à un autre, et donc choisir l'origine de ces branches comme on le souhaite.

Retour sur le commentaire du quadrilatère Convexe

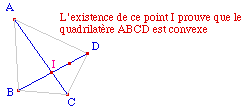
Le commentaire est là encore un nom, comme la droite de la page précédente, mais c'est le nom d'un point qui n'existe que si I existe. On considère le milieu de I et D (c'est le Pong) et le symétrique de I par rapport à ce point (Le Ping). Ainsi le commentaire - qui est le nom de ce nouveau point sur D - n'apparait que si I existe.

Placer un point logique sur un autre point

De la même manière dans la recherche d'un point qui caractérise que M est à l'intérieur d'un triangle, il est bien plus judicieux, pour les constructions qui en dépendront, d'avoir un point Int sous le point M au lieu d'être n'importe où dans le plan. Là encore, il suffit de prend le milieu de Int et de M et de faire le symétrique de Int par rapport à ce point. On obtient un nouveau point, sous M, appelé ici "est intérieur". IntTR2.fig

 On peut donc réaliser notre première macro logique, que l'on nommera dans la suite Ping-Pong qui à partir d'un point M et d'un point A, construit sur A un point qui est conditionné à l'existence de M.

Charger la macro Ping-Pong

Dans cette macro on indique d'abord le point conditionnel, puis le point sur lequel on souhaite que cette condition (d'existence) s'applique.

Le nom de Ping-Pong vient de ce qu'à l'origine, dans abraCAdaBRI papier, au lieu de construire le symétrique de M par rapport au milieu de M et A, on construisait le symétrique de A par rapport à M (Pong) puis le symétrique de ce point de nouveau par rapport à M (Ping).

On remarquera aussi l'utilisation du vocabulaire sous un point. En effet, dans la gestion des ambiguïtés, Cabri propose un petit PopUp menu qui liste les objets par ordre (chrono-)logique de construction. Ainsi un point logique est-il toujours sous le point à partir duquel il est construit.

La page suivante propose une première utilisation de la macro Ping-Pong.

 [1 - Nécessité de la Géométrie logique] [2 - L'existence comme critère logique] [4 - Un premier exemple]

Menu général