Image d'un point par une homothétie
(cas général)

 [Tangentes communes à deux cercles] [Retour "En Classe"]

 

L'objet de cette page est la réalisation d'une macro qui construit l'image d'un point M par une homothétie de centre O connaissant un point A et son image A'. Cette page existe car on y propose de construire une figure qui soit valide dans tous les cas, y compris si M est sur la droite (OA). En effet, dans une approche "papier" classique, on distingue deux cas, qu'il convient d'unifier pour que M' soit un unique point, que M appartienne ou non à la droite (OA).

 

Un construction dans le plan épointé

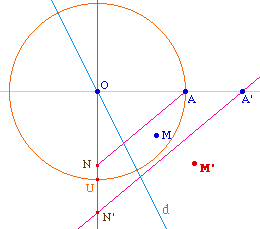
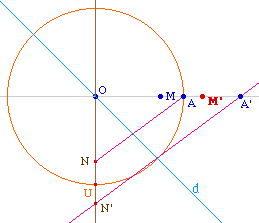
Soit donc une homothétie h de centre O dont l'image d'un point A est un point A'. On cherche une construction du point M', image d'un point M quelconque, indépendante du fait que M soit ou ne soit pas sur la droite (OA)

Le cercle de centre O passant par A coupe la perpendiculaire en O à (OA) en U. Soit d la bissectrice de l'angle UOM.

On note N le symétrique de M par rapport à d. Ce point N n'appartient à (OA) que si M est en O - et alors N aussi. Donc pour tout point M autre que O, l'intersection de la paralléle à (AN) passant par A' et de la perpendiculaire - (ON) sur l'illustration - existe. Soit N' ce point : par construction, c'est l'image de N dans l'homothétie h.

Alors le symétrique de N' par rapport à d est le point M' cherché.

La figure Imag1Pt.fig ci-contre.

Remarque : Si on observe cette figure, on remarquera que les points O, A et A' sont alignés sur une droite cachée. La construction se fait à partir de la droite (OA). En pratique, il ne faut donc appliquer la macro que dans le cas où elle a un sens : O, A et A' sont trois points alignés.

 

Il est clair que la construction est correcte pour tout point M - ici sur la droite (OA) - autre que O. Elle est donc plus générale qu'une application immédiate du théorème de Thalès.

La macro Homo1P.mac (objets initiaux O, A, A' et M)

Cette macro sera systèmatiquement utilisée dans le site quand on aura à construire l'homothétique d'un point dans cette situation.

 

  [Tangentes communes à deux cercles] [Retour "En Classe"]

 

Menu général