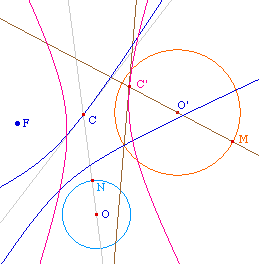
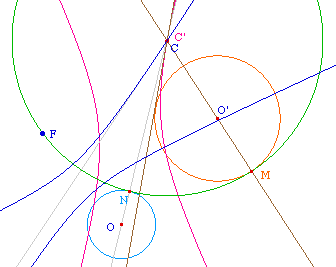
Soit un cercle C donné. On considère deux coniques ayant ce cercle pour cercle directeur associé au foyer F1 et F2 respectivement. Montrer - en réalisant la figure - que les tangentes communes de ces deux coniques - quand elles existent - sont constructibles à la règle et au compas.
 |
|