Exercices sur l'aspect bifocal des coniques
Solution de l'exercice P2

 

Etant donnés un point F et deux cercles C1 et C2, on se propose de construire à la règle et au compas les intersections communes des deux coniques ayant le point F comme foyer commun, et les cercles C1 et C2 comme cercles directeurs respectifs.

  

Phase d'analyse

a - préliminaire (reprise du coup de pouce)

Prenons une figure d'analyse ExpMFoy2.fig où l'on dispose de deux coniques de même foyer ayant deux cercles directeurs différents.

Soient M et N deux points des cercles directeurs, on construit les points des coniques C et C' associés, par intersection des droites (O'M) et la médiatrice de [FM] pour C', et l'intersection des droites (ON) et de la mdaitrice de [FO] pour le point C.

 

Puis déplaçons M et N sur les cercles directeurs pour que C et C' coïncident avec une des intersections des deux coniques

Alors le cercle centré sur l'intersection des deux médiatrices passant par F, par construction passe par M et N en étant tangent aux deux cercles directeurs.

Autrement dit, il semble bien que les points d'intersection des coniques soient les centres des cercles tangnets aux deux cercles directeurs passant par F.

 

On se souvient que ce problème a déjà été traité dans abraCAdaBRI, dans les exercices relevant de l'axe radical, plus précidément à cette page relative à la construction des cercles passant par un point A et tangents à deux cercles donnés.

Nous allons donc adapter un peu ... un exercice précédent.

b - sur les cercles passant par un point tangents à deux cercles donnés

Reprenons un extrait de la figure TC2C1PCn.fig de la page précédente CTgt2C1pt.html pour ne retenir que ce qui nous intéresse, les 4 points de contact des cercles solutions sur l'un des cercles. C'est la figure illustrée ci-contre :

SolP02a.fig dont on peut extraire la macro Cont4C.mac qui, étant donnés un point et deux cercles, renvoie sur le premier cercle cliqué les 4 points de contact des cercles passant par le point et tangents aux deux cercles (ci-contre U, U', V et V'). C'est cette macro qui sera utilisée pour la construction finale.

Pour une utilisation sur les tangentes communes en géométrie hyperboliques, on distinguera les points de contact de même type (2 contacts extérieurs ou deux intérieurs, U et U' ci-contre) de ceux de type contraire (un intérieur et un extérieur, V et V' ci-contre) pour faire deux macros distinctes :

ContMT.mac (pour Même Type : renvoie U et U')

ContAT.mac (pour Autre Type - ou types contraires : renvoie V et V')

Construction effective

 

 

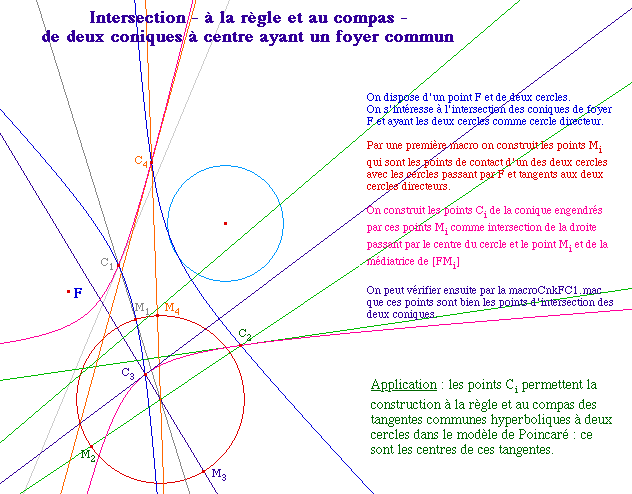
SolP02b.fig ou I2CnkMF.mac (renvoie les points Ci)

 

 

Retour à la page d'exercices

Menu général