Soit un cercle C donné, de centre O. On considère deux coniques ayant ce cercle pour cercle directeur associé au foyer F₁ et F₂ respectivement. Montrer - en réalisant la figure - que les tangentes communes de ces deux coniques - quand elles existent - sont constructibles à la règle et au compas.

Pour expérimenter autour de cet exercice et achever la construction on aura besoin de :

Charger la macro CnkFC1.mac qui construit une conique conaissant un foyer et le cercle directeur associé.

Analyse - conditions nécessaires

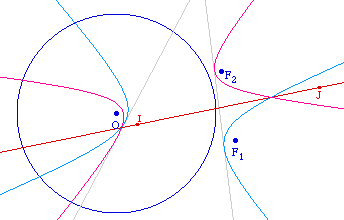
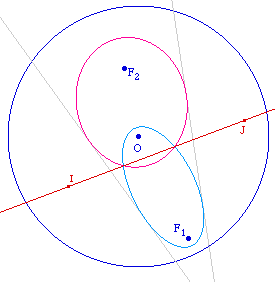
Les autres cercles directeurs des coniques sont les translatés du cercle C dont les centres sont F1 et F2. Si une tangente commune D existe, le symétrique de O par rapport à D doit être à l'intersection de ces deux cercles translatés. Supposons que les cercles se coupent en I et J, alors les tangentes communes aux deux coniques sont nécessairement les médiatrices de [OI] et de [OJ].

Construction - Illustration

 

En traçant les coniques avec la macro ci-dessus, on illustre bien que les deux médiatrices construites sont les tangentes communes. La figure SolP01G.fig ci-contre. On remarquera que ces coniques ne peuvent avoir que deux tangentes communes et non pas quatre car elles ne peuvent être entièrement extérieures l'une à l'autre ayant toutes les deux le point O comme foyer. Il est également clair que par construction, la droite (IJ) est la médiatrice des deux foyers F1 et F2.

Cas particulier

Si les foyers F₁ et F₂ sont exactement à une distance égale au diamètre du cercle directeur, il n'y a qu'une seule tangente commune :

Illustration ellipse - hyperbole

La figure SolP01P.fig propre à ce cas particulier.   C'est donc une façon de construire des coniques tangentes en un point à la régle et au compas, dans un cas particulier, celui de coniques de même cercle directeur. Enfin, si les foyers F1 et F2 sont séparés d'une distance supérieure au diamètre du cercle directeur, il n'y a plus de tangentes communes.

Illustration hyperbole - hyperbole

Complément : Points communs de coniques de même cercle directeur

On sait que les intersections d'une droite et d'une conique sont constructibles à la règle et au compas. Même si ce n'est pas "Cabri-pertinent" puisque l'intersection de coniques est un outil - non constructible - de Cabri, on peut néamoins remarquer, avec des arguments immédiats à écrire, que dans le cas de deux coniques de même type, les points communs aux deux coniques sont l'intersection de l'une d'elle avec la droite (IJ) médiatrice des deux foyers F₁ et F₂ . Ces intersections sont donc constructibles dans ce cas.

Cas de deux hyperboles

 

Cas de deux ellipses