Euclide lavé de toutes taches (1733)

Saccheri suppose connues les 28 premières propositions d'Euclide et reprend (? sans le citer ou redécouvre ?) le quadrilatère ABCD de Omar al-Khayyam ayant les angles en A et B droits et tel que AD = BC. Il prouve bien-sûr que les angles en C et D sont égaux. Saccheri fait alors trois hypothèses :

L'hypothèse de l'angle aigu : C = D inférieur à un droit. L'hypothèse de l'angle droit : C = D égal à un droit. L'hypothèse de l'angle obtus : C = D supérieur à un droit.

Propriété de la projection du milieu

Il montre ensuite que si une de ces hypothèses est vraie pour un quadrilatère, elle est vraie pour tous les quadrilatères, et il établit les résultats suivants (illustrés à l'attention lecteur de modèles bien entendu inconnus à cette époque) :

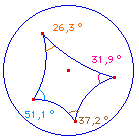
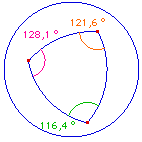
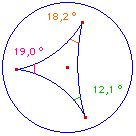
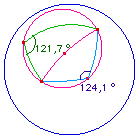
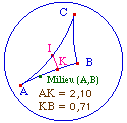
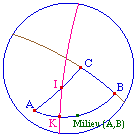
Hypothèse sur l'angle	Somme des angles d'un quadrilatère	Somme des angles d'un triangle	Angle inscrit dans un demi-cerle	Projection orthogonale du milieu d'un segment
AIGU	< 4 droits	< 2 droits	< 1 droit	AK > KB
DROIT	= 4 droits	= 2 droits	= 1 droit	AK = KB
OBTUS	> 4 droits	> 2 droits	> 1 droit	AK < KB

L'hypothèse de l'angle obtus

Puis Saccheri prouve le résultat suivant :

Dans l'hypothèse de l'angle obtus et dans celle de l'angle droit, une perpendiculaire à une droite donnée et une droite la coupant à angle aigu sont sécantes.

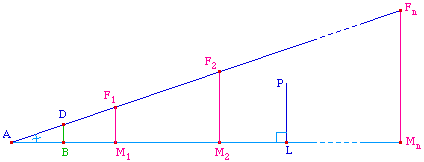
Soit (LP) et (AD) deux droites, l'une perpendiculaire à (AP) et l'autre faisant avec (AP) un angle aigu DAP.Sur (AD), construisons des segments AF₁ = 2AD, AF₂ = 2AF₁, ... et traçons les perpendiculaires (DB), (F₁M₁), (F₂M2), ... à (AP).
Alors, d'après ce qui précède, on a AM₁ „ 2AB, AM₂ „ 4AB, ... AM_n „ 2ⁿAB. Et donc, pour n assez grand, on aura AM_n > AP et la perpendiculaire (PL) qui coupe le côté (AMn) du triangle AM_nF_n doit aussi couper l'hypothènuse : les droites (LP) et (AD) sont sécantes.

 

Ceci permet à Saccheri d'exclure l'hypothèse de l'angle obtus. En effet, la conclusion implique le postulat d'Euclide qui lui-même aboutit à l'angle droit pour le quadrilatère de Saccheri. D'où la conclusion de Saccheri : "l'hypothèse de l'angle obtus est absolument fausse car elle se détruit elle-même".

Remarquons, toujours avec Jean Luc Chabert, qu'en fait, l'exclusion de la géométrie de l'angle obtus (la future géométrie elliptique de Riemann) par Saccheri est naturelle de par son utilisation de la demande 2 d'Euclide (Prolonger indéfiniment selon sa direction, une droite finie), avec une interprétation métrique de ce caractère infini des droites : on sait que sur la sphère, si les droites sont infinies, elle n'en reste pas moins bornées.

 

Hypothèse de l'angle aigu

Pour conclure à la preuve du postulat d'Euclide, Saccheri vient d'éliminer une première hypothèse. Reste à éliminer la seconde, l'hypothèse de l'angle aigu; pour cela, il se place dans le cadre de la figure précédente : une perpendiculaire et une oblique à une droite qui ne se coupent pas.

Saccheri déploie alors une fantastique rigueur logique pour travailler sur des figures loin de l'intuition ordinaire. En particulier, il ne fait pas d'hypothèses implicites comme tous ses prédécessuers et sait s'en tenir scrupuleusement à ses hypothèses.

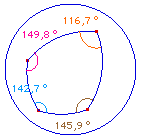
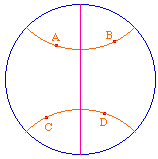La droite rose est la perpendiculaire commune aux deux droites (AB) et (CD).

Il montre alors que deux droites quelconques sont : soit sécantes, soit ont une perpendiculaire commune, soit sont asymptotes. C'est la classification que Lobachevsky retrouvera au siècle suivant. Il prend conscience que l'intuition pour les perpendiculaires communes, ne peut plus s'appuyer sur la figure euclidienne usuelle, comme le faisait Omar al-Khayyam, avec sa demande implicite sur les droites qui ne peuvent s'écarter des deux côtés à la fois, mais bien comme dans l'illustration ci-contre (au cercle horizon près bien entendu).

Les points idéaux de deux droites non connectables ont fait reculer Saccheri ...

Il va encore plus loin dans l'énoncé de véritables propriétés de géométrie non-euclidienne (de la géométrie hyperbolique) et précise en particulier la classification précédente en montrant ce qui sera, en fait, le point de départ de la théorie des parallèles de Lobachevsky, à savoir qu'étant donné un segment [AB], il existe un angle BAX vérifiant les propriétés suivantes : 1 - (AX) ne rencontre pas la perpendiculaire (BC) à (AB) en B. 2 - Toute oblique (AX') comprise dans l'angle BAX rencontre la perpendiculaire (BC). 3 - Toute oblique (AX") faisant un angle aigu plus grand que BAX avec (AB) a une perpendiculaire commune avec (BC). C'est à ce stade de son exposé que Saccheri n'a pas voulu franchir un pas de plus. Convaincu que la véracité du postulat d'Euclide, malgrés la finesse et la précision de tous ses raisonnements, il a préféré - préféré ! - voir là une contradiction (cette contradiction tant cherchée) en argumentant que les asymptotes (AX) et (BC) devraient avoir en leur point commun à l'infini - les futurs points idéaux de la géométrie absolue - une perpendiculaire commune, ce qui ne se peut. Et il a conclu, ici, par ce désormais fameux :

L'hypothèse de l'angle aigu est absolument fausse car cela répugne à la nature de la ligne droite.

Menu général