 |
|
 |
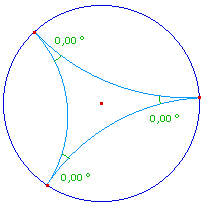 |
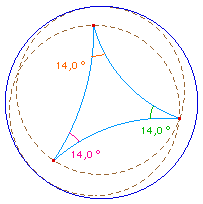
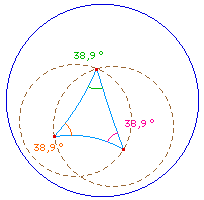
Il note d'ailleurs que lorsque la longueur du segment croît de 0 à l'infini, l'angle du triangle équilatéral décroit de 60 degrés à 0.Ci-contre un triangle hyperbolique équilatéral constitué de trois segments de longueur infinie dans le modèle de Poincaré : les sommets sont des points du cercle horizon, à l'infini pour ce modèle (points idéaux). : Pour trois points idéaux quelconque, l'aire du triangle hyperbolique vaut Pi.. |