Les mathématiciens arabes qui ont commenté la théorie des parallèles d'Euclide ont, en général, adopté l'équidistance comme définition du parallélisme. Montrer la proposition 29 des éléments d'Euclide sans recourir au cinquième postulat revient alors à élaborer une théorie du quadrilatère ayant deux angles droits.

Une preuve de Ibn al-Haytam (965 - vers 1040)

Soit ABCD un quadrilatère ayant 3 angles droits. Il s'agit de montrer que le quatrième angle est droit.

Dans cette preuve, al-Haytam utilise explicitement un résultat préalable, "montré" par le mouvement :

Le lieu des points équidistants d'une droite donnée et situés d'un même côté de cette droite est une droite.

qui est une propriété purement euclidienne ...

On peut noter également que al-Haytam, aprés l'ouvrage qui contient cette preuve, a écrit un second ouvrage "Sur la résolution de ce qui est douteux dans les Eléments d'Euclide" dans lequel il propose de remplacer le postulat par un autre "qui joue le même rôle et qui est plus clair" :

Deux droites qui se coupent ne peuvent être parallèles à une même droite.

Cet énoncé est par ailleurs équivalent à l'assertion de Proclus, déjà abordée :

Lorsqu'une droite coupe l'une des parallèles, elle coupe l'autre aussi.

Il est clair que le postulat proposé par al-Haytam remplace - sur le plan logique - effectivement le postulat traditionnel d'Euclide, mais puisqu'il le remplace, il ne l'évite pas, ce que croyait l'auteur : on reste en géométrie euclidienne. De plus, avec une définition des parallèles sur la base de l'équidistance, ces modifications permettent - et c'est important pour les auteurs arabes - d'éviter le recours explicite à l'infini. Reste qu'avec cette approche, l'existence des parallèles est posé ... et n'est pas résolu.

Une preuve de Omar al-Khayyam (1048 - vers 1123)

Les historiens des mathématiques retiennent de son "Commentaire sur les postulats problèmatiques du Livre d'Euclide", outre ses méthodes, surtout qu'elles ont probablement inspiré Saccheri puisque les quatre premières propositions de celui-ci, au XVII°siècle, sont identiques, selon K. Jaouiche, à celles de al-Khayyam, et que l'argumentation utilisée dans la troisème proposition est nouvelle - et sera reprise par Saccheri.

Cet auteur est très formaliste. Non seulement il rejette fortement l'utilisation du mouvement dans les démonstrations de ses prédécesseurs, mais il va même jusqu'à affirmer qu'il manque des axiomes aux éléments d'Euclide, et il propose ainsi d'ajouter :

Les grandeurs se divisent à l'infini et ne sont pas composées d'indivisibles.

Deux droites qui se coupent s'écartent l'une de l'autre à partir de leur point d'intersection.

Omar al-Khayyami étudie le quadrilatére ABCD ayant ses côtés [BC] et [AD] perpendiculaires à [AB] et ses côtés AD et BC égaux. Pour montrer la proposition 29, il faut commencer par montrer que, sous ces hypothèses, les angles C et D sont droits. Voici sa démarche :

Proposition 1 : Soient [AB] un segment, [AD] et [BC] perpendiculaires à [AB], tels que AD = BC. Alors les angles en C et D sont égaux. Proposition 2 : Soient ABCD comme dans la proposition 1, O le milieu de [AB], et [OR] la perpendiculaire à [AB] en O. Alors CR = RD et [OR] est perpendiculaire à [CD]. Proposition 3 : Sous les hypothèses de la proposition 2, les angles C et D sont droits. Les propositions 1 et 2 se démontrent simplement, dans le style d'Euclide, sans le postulat. On notera que la situation est différente de la projection du milieu rencontrée chez Aganis. Avec un vocabulaire contemporain, on dirait simplement que (OR) est la médiatrice de [AB], et que la symétrie orthogonale par rapport à (OR) transforme [BC] en [AD], et donc C en D. Nous allons donc observer la démarche de Omar al-Khayyam dans la troisième proposition.

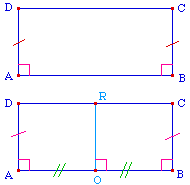
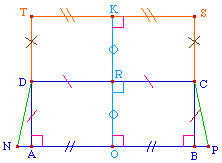
Il commence par prolonger le segment [OR] d'une longueur égale : RK = OR, et trace la perpendiculaire à (OK) en K. Cette droite coupe (BC) et (AD) en S et T. Il montre alors que CS = DT et donc, d'aprés ce qui précède, on a aussi KT = KS. Omar al-Khayyam fait alors successivement l'hypothèse que les angles égaux BCD et ADC sont aigus, puis qu'ils sont obtus. Il obtient deux contradictions, il en déduit alors que ces angles sont droits. 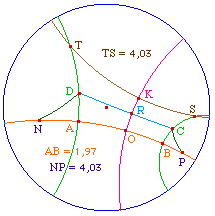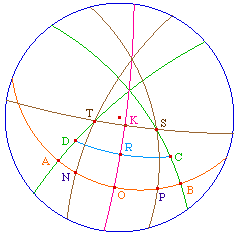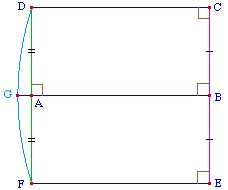Etudions le cas aigus : Par "rotation autour de (CD)" - c'est-à-dire par symétrie orthogonale - [RK] vient sur [RO], (ST) sur (AB) et le segment [ST] sur un segment [PN]. L'angle SCR étant supérieur à l'angle aigu BCR, la longueur ST, égale à PN, est plus grande que AB. Ainsi, remarque al-Khayyam, les droites (BC) et (AD), perpendiculaires à (AB) s'écarteraient d'un côté de (AB) ; mais pour des raisons de symétrie, elles s'écarteraient aussi de l'autre côté.

De la même manière, si les angles égaux BCD et ADC étaient obtus, on monterait que la longueur ST est plus grande que AB, et donc les droites (BC) et (AB) se rapporcheraient l'une de l'autre des deux côtés de (AB).

Ainsi, conclut Omar al-Khayyam, les angles en C et D sont droits car les deux cas, aigu et obtus contredisent l'idée que l'on a des droites :

Deux droites ne peuvent pas s'écarter l'une de l'autre des deux côtés à la fois, ni se rapprocher des deux côtés à la fois.

Jean Luc Chabert fait remarquer qu'en plus de cette propriété des droites explicitement mentionnée, l'auteur utilise aussi l'existence des points d'intersection S et T qu'il justifie par le fait que la distance entre deux parallèles ne varie pas (en fait "distance bornée" suffirait).

On voit, avec cet auteur, d'une part que des ingrédients pour la découverte des comportements hyperboliques sont déjà présents, et d'autre part, combien le recours au monde sensible comme support des concepts reste malgrés tout prégnant, même chez un auteur réputé particulièrement formaliste. Observons la construction de Omar al-Khayyam dans un modèle hyperbolique (celui du disque de Poincaré) et un modèle elliptique :

Illustration de l'inégalité AB < TS dans le cas hyperbolique Comm01.fig (PC) ou Comm01M.fig (Mac)

Les points T et S peuvent ne pas exister, car la distance entre deux parallèles n'est pas borné.

Cas elliptique (les parallèles n'existent pas)

Comm02.fig (PC) ou Comm02M.fig (Mac)

 

 

[Commentateurs] [Commentateurs grecs] [Commentateurs européens] [Précurseurs]

[Présentation chronologique] [Equivalences du V° postulat] [Le livre I d'Euclide]

[Retour aux GNE] [Références utilisées]

Menu général