Proposition 17 : Q
=> P
Deux angles d'un
triangle quelconque, de quelque manière qu'ils
soient pris, sont moindres que deux droits
|
<= Réciproque
=>
|
Cinquième
postulat : P => Q
Si une droite, tombant
sur deux droites, fait les angles intérieurs
d'un même côté plus petits que deux
droits, ces droites, prolongées à
l'infini, se rencontreront du côté
où les angles sont plus petits que deux
droits.
|
|
|
Raisonnement par l'absurde
pour obtenir la contraposée
|
|
|
|
|
|
Raisonnement par l'absurde
pour obtenir la contraposée
|
|
|
Proposition 27 : non P
=> non Q
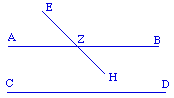
Si une droite, tombant
sur deux droites, fait des angles alternes
égaux entr'eux, ces deux droites seront
parallèles.
|
<= Réciproque
=>
|
Proposition 29 : non Q
=> non P
Une droite qui tombe
sur deux droites parallèles, fait les angles
alternes égaux entr'eux, l'angle
extérieur, égal à l'angle
intérieur opposé et placé du
même côté, et les angles
intérieurs placés du même
côté, égaux à deux
droits.
|
Le raisonnement de Proclus semble être celui-ci : la
proposition 17 a été montrée par Euclide sans
recours au postulat. Alors cette cinquième demande doit
aussi pouvoir être montrée. Proclus aborde donc cette
preuve là où le postulat apparaît pour la
première fois, à la proposition 29.