L'axiome énoncé par Wallis (1616 - 1703)

Pour une figure quelconque, il en existe toujours une autre, de grandeur quelconque, qui lui soit semblable.

La preuve proposée

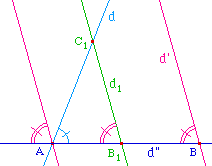
Soient d et d' deux droites, coupées en A et B par la droite d". On suppose que les angles intérieurs a et b d'un même côté de d" ont pour somme a+b, plus petit que deux droits. On veut alors montrer que les droites d et d' sont sécantes. Par A menons la droite d1 de sorte que d' et d1 forment avec la droite d" des angles correspondants égaux. Il est clair que d1 se trouve dans l'angle adjacent à l'angle a. À présent, déplaçons la droite d' continûment le long du segment [AB] de sorte que l'angle qu'elle fait avec d" reste toujours égal à b. Avant qu'elle n'atteigne sa position finale d1, elle doit nécessairement couper d, ce qui détermine un triangle AB1C1 dont les angles en A et B1 sont respectivement égaux à a et b. Sur [AB], construisons un triangle ABC semblable à AB1C1. Ainsi, les droites d et d" se coupent au point C.

Remarques

En fait, Wallis utilise un axiome plus faible que celui demandé :

Sur un segment donné, on peut construire un triangle semblable à un triangle donné.

On notera tout d'abord que l'axiome de similitude est une idée originale de Wallis qui n'existe pas chez les autres commentateurs d'Euclide. Pour les historiens, c'est d'ailleurs la seule de cette époque, avant les travaux de Saccheri.

Wallis utilise le mouvement, en particulier le déplacement continu, contrairement à l'usage en géométrie, et en particulier à la démarche d'Euclide où seules les positions initiales et finales sont ordinairement considérées.

Sacherri montrera toutefois qu'il est possible d'utiliser la méthode de Wallis, dans un style purement euclidien, pour montrer le cinquième postulat, sous la simple hypothèse :

Il existe deux triangles non égaux (ie non superposable) ayant leurs angles deux à deux égaux.

Wallis expose aussi une preuve de Nasir ad-Din at-Tusi, issue de la publication en arabe de son traité en 1594 à Rome. Cette preuve est proche de celle de Omar al-Khayyam, mais il utilise comme propriété première des droites :

Si deux droites s'inclinent l'une sur l'autre dans une direction, elles continuent à s'incliner l'une sur l'autre dans cette direction.

Il reviendra à Saccheri de s'apercevoir que cette propriété n'est pas une notion première des droites, mais encore une propriété qui découle de la théorie euclidienne des parallèles.

  

Menu général