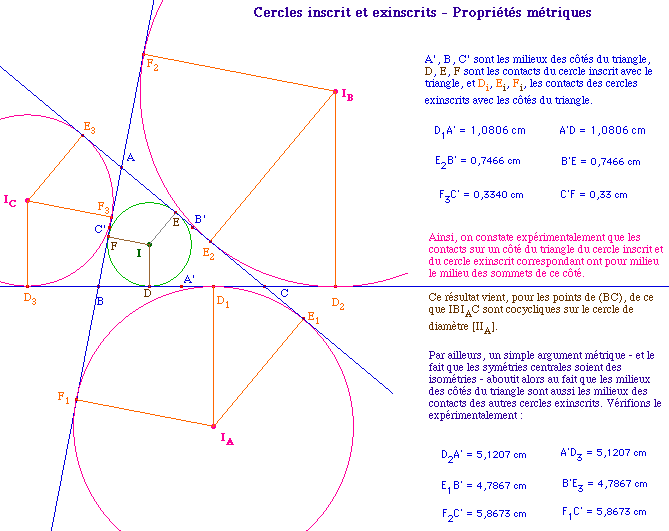
3 - Propriétés des points de contact
[Présentation
générale] [1 -
Définitions des bissectrices] [2
- Pieds des bissectrices]
[4 - Diverses relations
métriques] [5 -
Théorème de Feuerbach]
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I

Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
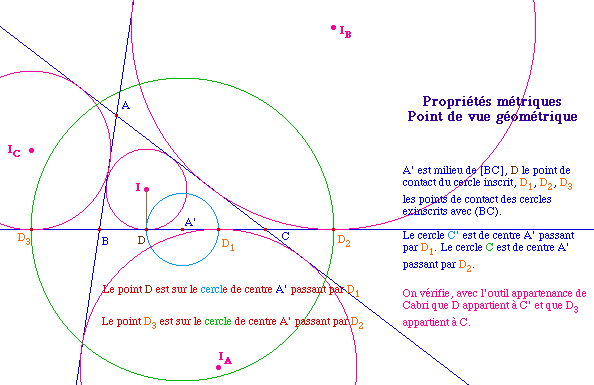
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
|
|
Notons P1 l'intersection de la bissectrice intérieure issue de A et du cercle circonscrit à ABC, de centre O. Alors BP1C est isocèle en P1 car en angle géométrique on a, P1BC = P1AC = BAP1 = BCP1. Donc P1 appartient à la médiatrice de [BC].Par ailleurs, les points I, B, C, IA sont
cocycliques sur le cercle de diamètre
[IIA]. Or le centre est à la fois
sur la bissectrice (AI) et sur la médiaitrce de
[BC]. Ainsi, si le triangle n'est pas isocèle
en A (ie si ces deux droites sont distinctes), le centre de
ce cercle est l'intersection des deux droites, c'est
à dire le point P1.
|
On peut aussi remarquer, sans utiliser le point P1, que dans ce cas, A' = D = D1. |
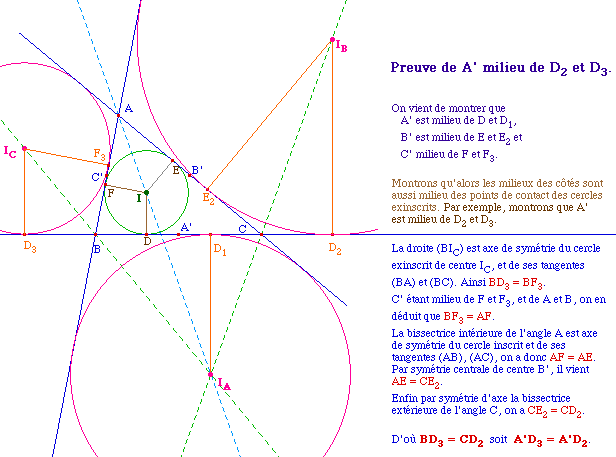
Cette dernière preuve est purement métrique et s'applique entièrement à la géométrie hyperbolique. Par contre ce n'est pas le cas de la première partie (pourtant vraie elle aussi).
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
 |
à partir des points de contact |
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
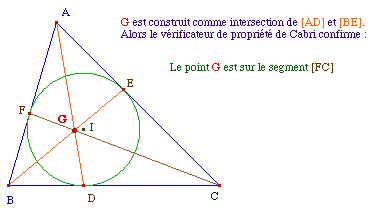
|
PreuveElle peut se faire par les barycentres. En notant traditionnellement a = BC, b = AC, c = AB, et le demi-périmètre p = (a+b+c)/2.On trouve rapidement G barycentre de
Autre approche (par un cas particulier du théorème de Carnot) : utilise qu'un cercle est une conique affine particulière. |
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
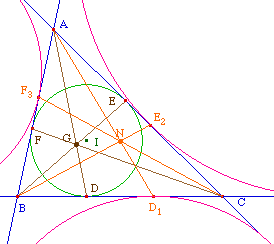 |
PreuvePuisque le cercle exinscrit associé à l'angle A - de centre IA - est tangent à (BC) en D1 symétrique de D par rapport au milieu A' de [BC], les droites ainsi construites (AD1), (BE2) et (CF3) sont concourantes comme isotomiques des droites (AD), (BE) et (CF). En particulier elles sont concourantes en un point N, isotomique du point de Gergonne, appelé point de Nagel, il a pour barycentre (notations ci-dessus) :
|
Résultat | Cabri-vérification | Preuve | Conséquences | Point de Gergonne | Point de Nagel | Lien avec O, H, I
|
|
Preuve
Remarque : sur l'illustration ci-contre (HN) est parallèle à (BC) seulement pour l'esthétique de la figure, ce n'est bien-sûr pas une propriété générale. |
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]