 |
|
6 - Céviennes et points isotomiques
[1 - Aspect historique] [2 - Preuve du théorème] [3 - Cas des céviennes] [4 - Cas des points symétriques]
[5 - Cas des points doubles] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]
 |
|
|
|
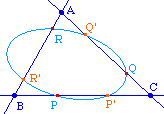
aux milieux des côtés |
|
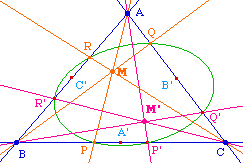
D'après le théorème de Carnot, dans le cas particulier des points symétriques, les 6 points sont sur une coniques. Puisque, par hypothèse on a :Il en résulte :
|
Ce résultat se montre bien entendu classiquement avec les barycentres. Il s'agissait ici de retrouver ce résultat sans calcul barycentrique, juste par une conique intermédiaire, grâce au théorème de Carnot.
|
|
Dans le cas où les céviennes de départ sont parallèles, nécessairement les céviennes isotomiques sont concourantes.En efet, dans la situation ci-dessus, siavec nécessairement
|
Dans la page 8, on verra par exemple que le point de Nagel est l'isotomique du point de Gergonne.
abraCAdaBRI est intéressé par d'autres applications de l'isotomie en général que les lecteurs pourraient avoir en tête, d'un point de vue affine ou projectif si possible (plutôt qu'euclidien).
[1 - Aspect historique] [2 - Preuve du théorème] [3 - Cas des céviennes] [4 - Cas des points symétriques]
[5 - Cas des points doubles] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]